Bonjour je suis la maman d une élève en prepa ecs1 qui est un peu débordée et prete a craquer je suis moi même prof de math au collège et je voudrais l aider mais je suis un peu dépassée . Je vous explique mon pb
On pose ck= somme cos px pour p allant de 1 à k
Montrer par récurrence que ck =(cos ((k+1)x/2).sin((kx)/2))/ sin(x/2) pour x different 2hpi h
Puis en déduire que (ck) est bornée
Merci mille fois pour votre aide si vous pouvez m aider
j'ai su le faire à partir de la partie réelle de la somme des e(ikx) mais pas par récurrence
Trigo
12 messages
- Page 1 sur 1
imalefette a écrit:merci beaucoup[B] j 'y suis arrivée comme cela en revisant un peu (!!!!) mais pas par récurrence ? et je n'arrive pas à montere proprement qu'elle est bornée
Oui, excusez moi je n'avais pas vu que vous vouliez une récurrence...
Pour le côté "bornée" il faut bien comprendre que l'on vous demande de montrer qu'elle est bornée en k. Or, si
Pour la récurrence, je regarde...
Bonjour,
Pour la récurrence :
Supposons la propriété vraie au rang k et montrons là au rang k+1.
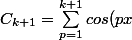=\sum_{p=1}^k cos(px)+cos(k+1)x)
par hypothèse de récurrence on a :
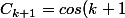x/2\, \frac{sin(kx)/2}{sinx/2}+cos(k+1)x)
Ensuite je raisonne en partant du résultat (faudrait l'écrire à l'envers pour être rigoureux ...)
On veut montrer que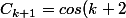x/2\, \frac{sin(k+1)x/2}{sinx/2})
On écrit :
x/2\, \frac{sin(kx)/2}{sinx/2}+cos(k+1)x\, =\, cos(k+2)x/2\, \frac{sin(k+1)x/2}{sinx/2})
En multipliant tout par on obtient :
on obtient :
x/2\, sin(kx)/2+cos(k+1)x\, sin x/2\, =\, cos(k+2)x/2\, sin(k+1)x/2)
Et là en utilisant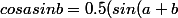/2+sin(a-b)/2))
et = -sinb)
on simplifie l'égalité en :
x/2-sin x/2)\, +\, 0.5(sin(2k+3)x/2-sin(2k+1)x/2)\, =\, 0.5(sin(2k+3)x/2-sinx/2))
Ce qui fait 0=0 ^^
l'égalité est donc vraie, la propriété est héréditaire et donc elle est vraie pour tout k.
(Bon sûr bien pour écrire ça proprement il faudrait partir du membre de gauche et transformer avec les formules de trigo pour obtenir le membre de droite, mais j'ai fait au plus court).
Ensuite on en déduit :

Pour la récurrence :
Supposons la propriété vraie au rang k et montrons là au rang k+1.
par hypothèse de récurrence on a :
Ensuite je raisonne en partant du résultat (faudrait l'écrire à l'envers pour être rigoureux ...)
On veut montrer que
On écrit :
En multipliant tout par
Et là en utilisant
et
on simplifie l'égalité en :
Ce qui fait 0=0 ^^
l'égalité est donc vraie, la propriété est héréditaire et donc elle est vraie pour tout k.
(Bon sûr bien pour écrire ça proprement il faudrait partir du membre de gauche et transformer avec les formules de trigo pour obtenir le membre de droite, mais j'ai fait au plus court).
Ensuite on en déduit :
imalefette a écrit:je ne sais pas si je peux oser mais je bloque aussi sur cet exo, en fait je n'arrive même pas à le démarrer le but est de montrer que l'on peut exprimer cos(nx) en fonction d'un polynome en cosx ie cos(nx)=Pn(cosx)
remarque si P(X)=X^2+X+1 alors P(cosx)=....
déterminer P0(X) et P1(X)
merci bcp
Là encore on peut utiliser la formule de Moivre avec celle de Newton :
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
