Transformées de Fourier et fenetrage

[beserum]

Bonjour a tous,

Voila, j'ai bien compris la démo (résolution plutot) du fenetrage, dans le cas de la transformée d'un rectangle en temporel.

Si on a
x(t) =
{ 1 pour |t|<=T1
{ 0 pour |t|>=T1

la transformée s'écrit

X(jw) = intégrale de ( e^(-jwt) dt) dont les bornes sont -T1 à T1
Ce qui donne une une primitive : [ (-e^-jwt)/jw] = [ (j e^-jwt)/w] dont les bornes sont toujours les mêmes.

Ensuite si je developpe j'obtiens = (j/w)( (e^-jwT1) - (e^-jwT1)

Ensuite comme je n'ai qu'à developper les e^machin sous la forme de sin et cos, j'ai les cos qui se simplifient et finalement j'obtiens

2 sin (wT1) / w comme transformée de Fourier de ma fenetre

ça, ça va, mais mon probleme c'est quand j'ai cette fois une fenetre DISCRETE
(comme x[n] = 1 pour |n|<=2, 0 sinon)

je sais que ma transformée cette fois est égale a
X(e^jw) = (sin ( (2+2+1 = période) (w/2)) / (sin (w/2))

mais je n'arrive pas a le trouver, en partant de la definition d'une transformée de Fourier Discrete-continue.

(= somme de moins l'infini à plus l'infini des x[n].e^(-jwn) )

Je me doute qu'il s'agit aussi de réecrire les exponentielles sous forme de sinus et cosinus, mais je tourne en rond.

Merci de m'expliquer si quelqu'un connait le cheminement (et si mes equations sont lisibles :lol2:)

[mathelot]

Bonjour,


si l'angle w est commensurable avec , donc pas de la forme :zen: mais une fraction du style

les exponentielles forment un sous-groupe discret cyclique du cercle unité.

On écrit alors l'image de la transformée de Fourier discrète
comme un système nxn que l'on résoud par inversion
est proportionnele à

cf l'algo de FFT (fast fourier transform) où on particularise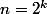

tout ceçi est bien expliqué dans un merveilleux bouquin, à lire absolument:

"l'algèbre discrète de la transformée de Fourier" de Gabriel Peyré
chez Ellipse semble-t-il


euh, sinon, si n appartien à Z, les formules d'inversion doivent marcher
en remplaçant les intégrales par des séries et en intervertissant les signes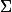

il est plus simple de travailler avec des exponentielles qu'avec sin et cos.
les exponentielles forment un système orthogonal pour un produit scalaire
avec intégrale. on doit pouvoir calculer les coeff ??