Bonsoir, notre prof nous a donné un exercice avec notamment comme question:
J={(x,y) E R^2| x^2+y^2<4, y>1, y<2-x}
1) Dessiner J
2) Montrer qu'il est ouvert en l'exprimant comme l'union ou l'intersection des boules ouvertes.
Merci d'avance.
Topologie Espaces vectoriels normés
5 messages
- Page 1 sur 1
Re: Topologie Espaces vectoriels normés
Bonjour
C'est un peu tordu comme exercice: montrer quelque chose d'évident en faisant compliqué.
Bref, toutes les boules ci-dessous sont des boules ouvertes avec comme distance la distance euclidienne.
Soit
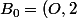)
Soit maintenant les points
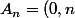) et
et 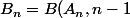 , n=2,3,....)
Les points
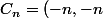, n=0,1,2,....) . et les boules
. et les boules \sqrt{2}))
Alors
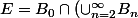 \cap ( \cup_{n=0}^{\infty} \tilde{B} _n))
C'est un peu tordu comme exercice: montrer quelque chose d'évident en faisant compliqué.
Bref, toutes les boules ci-dessous sont des boules ouvertes avec comme distance la distance euclidienne.
Soit
Soit maintenant les points
Les points
Alors
Re: Topologie Espaces vectoriels normés
Merci beaucoup pour votre réponse, malheureusement je bloque aussi sur la première question qui est de dessiner l'ensemble je ne sais pas comment m'y prendre ?
Re: Topologie Espaces vectoriels normés
Et bien
x^2+y^2<4 c'est la boule B_0.
y>1 c'est un demi-plan (tracer y=1)
idem y<2-x (tracer y=2-x)
x^2+y^2<4 c'est la boule B_0.
y>1 c'est un demi-plan (tracer y=1)
idem y<2-x (tracer y=2-x)
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
