Theorie groupe

[oumou]

bonsoir , est ce que quelqu un aurait il une idee sur cette question SVP ( ca m`a bloque dans un sujet de controle continu ) la voici :

Soit H l ensmble des matrices de la forme , p . montre que H est cyclique , c est a dire engendre par un element .Est il distingue ?



Merci d avance

[zygomatique]

salut

il manque une information fondamentale : quelle opération est considérée ?

s'il est cyclique alors tu peux l'engendrer par un seul élément ...

tu n'as pas une petite idée sur cette élément ?

[oumou]

on est dans GL(2,R) , de groupe de matrice (2,2) inversibles a coefficient reels.

euhh non pas du tout

[oumou]

j ai viens de voir quelque part a l instant que H est engendre par la matrice et donc H est cyclique
mais je ne sais pas comment ils ont pu determiner cette matrice ! pourriez vous m explique svp?

[samoufar]

Bonjour,

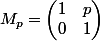
Note pour tout . Que vaut alors pour ? Que vaut ?

Donc en particulier, que vaut pour ? Donc pour quelle valeur de peut-on ainsi obtenir toutes les matrices de ?


PS: @zygomatique : Il s'agit forcément de la loi de multiplication puisque la loi d'addition n'est pas interne à .

[Ben314]

Salut,
Et pour "plussoyer" concernant ce que dit samoufar çi dessus, je rajouterais que, pour montrer que "H est cyclique", ben ça semble quand même on ne peut plus normal de commencer par montrer que H est un groupe ou, plus précisément, que c'est un sous groupe de GL(2,R).
Et cela conduit inévitablement à commencer par faire les calculs préconisés par samoufar.

[oumou]

elle vaudra peut etre la matrice identite 2 , j en ai vraiment aucune idee

[Ben314]

elle vaudra peut etre la matrice identite 2 , j en ai vraiment aucune idee

?????????

[zygomatique]

Bonjour,

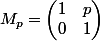
Note pour tout . Que vaut alors pour ? Que vaut ?

Donc en particulier, que vaut pour ? Donc pour quelle valeur de peut-on ainsi obtenir toutes les matrices de ?


PS: @zygomatique : Il s'agit forcément de la loi de multiplication puisque la loi d'addition n'est pas interne à .

je m'en doute bien ... et le msg suivant de ben314 permettait tout comme le tien ici présent de se rendre compte de ce qui se passe quand on multiplie deux telles matrices et de répondre à la question ... tout seul ...