Theorie de groupe

[oumou]

Bonjours !!

Nous venons de commencer les structures algébriques et ce n'est pas simple ! Voila mon exercice, j'espère que vous pourrez m'aider un peu dans la démarche à suivre..

1. soient definie par f(x) = .
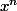
montre que f est un morphisme du groupe dans lui meme . (j ai pu repondre sans difficulte )
en determiner son image de son noyau .

2. justifier que exp : est un morphisme du groupe de (C,+) vers (C*,x) .
( je dis soit tq f (x) = exp(x) , f(x+y)= exp (x+y) = exp (x) x exp(y) = f(x) x f(y) )
en determiner son image et son noyau .

[Ben314]

Salut.
Deux remarques :

- Tel quel, l'énoncé de l'exercice 1) est très incomplet et même faux. Lorsque l'on parle de morphisme de groupe, il faut évidement savoir de quel groupe il s'agit, c'est à dire non seulement connaitre l'ensemble sur lequel est défini la structure de groupe, mais aussi quelle est l'opération qui muni cet ensemble d'une structutre de groupe. Là, vu la question posée, je suppose que le groupe, c'est R* muni de la multiplication mais, bien entendu, on peut munir l'ensemble R* (de tonnes) de lois autres que la multiplication dont (des tonnes) qui vont donner une structure de groupe et x->x^n ne sera un morphisme de groupe que pour certaines d'entre elles.
Donc, si, comme dans le cas présent, on te donne pas la loi, ben tu risque pas de savoir si c'est ou pas un morphisme de groupe. Sans parler du fait que si tu prend comme dans l'énoncé R tout entier et pas R* comme ensemble d'arrivé, je suis à peu près persuadé que tu ne trouvera pas de structure de groupe sur R tout entier qui fasse que x->x^n soit un morphisme de groupe de R* dans R.
Enfin bref, l'énoncé du 1) c'est "du grand n'importe quoi".

- Oukélé la question que tu pose ?

[oumou]

- ah oupss!!! je ne me suis meme pas rendu compte desole c est plutot montre que f est un morphisme du groupe (R*, x )dans lui meme .

-comment determiner son image et son noyau ?

[Ben314]

C'est quoi la définition de "l'image d'un morphisme de groupe" ?
du "noyau d'un morphisme de groupe" ?

Sinon, les maths, c'est comme le Français (ou les autres langues) : tu prend une phrase (ou un énoncé) tout ce qu'il y a de plus cohérent, tu enlève "au pif" des mots et tu obtient en général du charabia dénué de sens, voir même, si tu as pas de pot un truc qui a du sens, mais pas du tout le même que celui de la phrase de départ...

Et en maths., c'est fréquemment encore plus "fâcheux" qu'en Français vu que pour raccourcir le discours, on abrège au maximum : juste une petite * à coté de R (pour traduire "privé de zéro") oublié et c'est tout le sens de l'expression qui change...

[oumou]

oui , effectivement

- im f = { y, il existe x tq y = f(x) } ou f : G H un morphisme de groupe et
ker f = { x tq f(x)= e}