Théorie du contrôle et convexité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 21 Nov 2008, 18:21
par nemesis » 21 Nov 2008, 18:21
Bonsoir à tous,
je voudrais démontrer que l'espace des contrôles

, qui transfèrent a en b au temps T c.à.d
 \text { tel que } y^{a,u} (T) =b })
est un espace convexe fermé et non vide de
)
pour le non vide, on sait qu'il existe toujours un contrôle qui transfert a en b, dans cet espace
mais comment faire pour la convexité et pour la fermeture, j'ai essayé mais je crois que je me suis embourbé dans les calculs,
si quelqu'un peut m'aider
merci d'avance
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 21 Nov 2008, 18:50
par nemesis » 21 Nov 2008, 18:50
c'est bon pour la convexité, une petite aide pour la fermeture ??
:)
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 22 Nov 2008, 18:22
par nemesis » 22 Nov 2008, 18:22
toujours pas d'idées ? :)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 22 Nov 2008, 18:50
par ffpower » 22 Nov 2008, 18:50
C est quoi

-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 22 Nov 2008, 19:00
par nemesis » 22 Nov 2008, 19:00
c'est la solution du système qui transforme l'état a en b au temps T, en prenant comme contrôle, u.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 22 Nov 2008, 19:06
par ffpower » 22 Nov 2008, 19:06
Cad?c quoi un controle?Enonce précisément le probleme,et t aura p-e des réponses
-
nemesis
- Membre Relatif
- Messages: 343
- Enregistré le: 23 Sep 2006, 15:28
-
 par nemesis » 22 Nov 2008, 19:15
par nemesis » 22 Nov 2008, 19:15
ah d'accord, je vois,
en fait on essaye de résoudre un système d'équations différentielles qui dépendent d'une fonction u, cad ce système
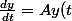 + B u(t))
avec comme condition initiale
=x)
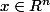
et
)
et
)
et en faite, puisque la solution dépendra de u, alors on cherche a contrôler la solution, cad trouver le contrôle u avec lequel on aura, en imposant un état initial a, un état final b, au bout d'un certain temps T d'où
 =b)
voili voilou, si ça inspire quelqu'un ...

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
