Théorème de point fixe de Brouwer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 10 Nov 2012, 10:16
par acoustica » 10 Nov 2012, 10:16
Bonjour,
Une question qui me taraude depuis un certain temps : le théorème du point fixe de Brouwer, souvent présenté dans un espace compact et convexe, est-il valable dans un espace homéomorphe à une boule unité fermée ? Car après tout, j'imagine que dans une tasse en forme de haricot (non convexe), notre cher Brouwer trouvera un point fixe à la surface de son café de la même façon non ?
Joli photo made home :

J'ai voulu appliquer le théorème qui nous dit que pour A une partie convexe et bornée d'un espace vectoriel normé E de dimension finie, alors l'intérieur de A, son adhérence et sa frontière sont homéomorphes respectivement à la boule unité ouverte, à la boule unité fermée et à la sphère unité de E.
Mais qui ne nous est en fait d'aucun secours^^.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 10 Nov 2012, 11:40
par cuati » 10 Nov 2012, 11:40
Bonjour,
une idée comme ça :
Soit A un compact homéomorphe au disque unité fermé D d'un espace euclidien. Ta question revient donc à savoir si une fonction continue
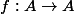
possède un point fixe. J'aurai tendance à dire que si
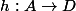
est un homéomorphisme alors
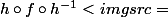
\rightarrow D"/> est continue et donc d'après notre théorème il existe
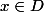
tel que
=x)
et donc
=h^{-1}(x))
et
)
est un point fixe de

dans

.
L'idée me parait (un peu trop?) simple mais je dois avouer que je n'ai pas revu la démonstration du théorème du point fixe de Brouwer depuis
très longtemps... ce qui est sûr c'est que si l'espace n'est pas connexe cela ne marche pas (il y a des contre-exemples simples) et en dimension infinie non plus (contre-exemples classiques...)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Nov 2012, 14:29
par Doraki » 10 Nov 2012, 14:29
Ben oui la propriété "pour tout f continue X -> X, f admet un point fixe" est purement topologique, donc si X est homéomorphe à Y, X vérifie la propriété si et seulement si Y la vérifie aussi.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 10 Nov 2012, 18:57
par acoustica » 10 Nov 2012, 18:57
Merci à vous deux pour vos réponses ! Oui effectivement, ça me paraît plus clair maintenant !
 par vitaliParadox » 25 Juin 2014, 14:23
par vitaliParadox » 25 Juin 2014, 14:23
Pour répondre à Cuati;
Comme le précise Doraki, la propriété f:X->X continue admet un point est topologique. Ainsi, le théorème du point fixe de Brouwer marche aussi pour les ensembles homéomorphes à la boule unité de R^n. Concernant les parties compactes et convexes d'un espace euclidien, ils ne sont pas obligatoirement homéomorphes à la boule unité. Par contre; on peut calquer la démo figurant dans le livre de Godbillion. Dans le cas où l'espace est de dimension 2, on montre d'abord que le bord d'une telle partie n'est pas simplement connexe et que la partie compacte et convexe de R^2 est simplement connexe. Ainsi, il ne peut y avoir de rétraction de l'ensemble dans son bord. La convexité permet justement de construire une rétraction si jamais il y avait une fonction continue ne satisfaisant pas la propriété du point fixe. Pour les dimensions supérieures, cela utilise les cohomologies de De Rham. On doit pouvoir montrer (en utilisant le théorème de changement de variable dans l'intégrale pour se ramener à une intégrale sur une sphère ou quelque chose dans le genre), que l'algèbre de cohomologie de rang n (la dimension de l'espace) du bord est R tandis que celle de l'ensemble est 0 et donc pas de rétraction.
Espérant avoir un peu éclairci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités

