Bonjour,
Je suis en train de plancher sur un exercice du Rudin "analyse réelle et complexe", exercice 16 du chapitre 3 "espaces
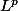
", et j'ai un problème avec la dernière question.
Le théorème d'Egoroff dit que si la mesure de

est finie, et si
:E\rightarrow\C)
est une suite de fonctions mesurables convergeant (presque partout) vers

, alors on peut trouver pour n'importe quel

une partie
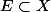
telle que
)
converge uniformément sur

et
<\varepsilon)
Pour cette partie, c'est bon j'ai la démonstration. C'est la suite qui m'embête.
Rudin dit alors "Avec essentiellement la même démonstration, montrer que le théorème ne se généralise pas au cas où
)
est remplacée par
)
avec
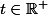
" (donc, une famille de fonctions et non plus une suite, avec toujours le même principe de la convergence simple quand t tend vers l'infini)
Le problème, c'est que "avec essentiellement la même démonstration" j'arrive au même résultat. Voici la démonstration en question : ai-je fait une erreur ?
Pour tous
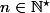
et
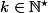
, je pose
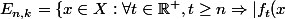-f(x)|<\dfrac{1}{k}\})
Pour

fixé, les
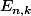
forment une suite croissante (au sens de l'inclusion) d'ensembles dont la réunion est égale à

(puisque
)
converge simplement vers

donc pour tout

il existe un rang t à partir duquel son image par
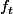
est toujours inférieure à 1/k (on peut également étendre à "converge pp", cela ne change rien)
Comme X est de mesure finie, il s'en suit qu'il existe un certain
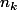
tel que
<\varepsilon 2^{-k})
(où

est la mesure). On se débrouille alors pour que
)
forme une suite croissante (toujours possible car si un
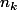
convient, tout

plus grand convient également).
On pose alors
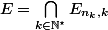
et on remarque que la mesure de son complémentaire est inférieure à la somme des mesures des complémentaires des
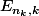
:
=\mu\Big(\bigcup_{k\in\N^\star}(X\setminus E_{n_k,k}\Big)\leq \sum_{k\in\N^\star}\varepsilon 2^{-k} = \varepsilon)
Et par construction, tout

appartient à tout
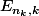
Donc pour tout
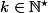
, on trouve bien un réel positif

(en fait
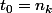
) tel que
-f(x)|<\dfrac{1}{k})
Ce qui est bien la convergence uniforme sur

...
Alors, ai-je raté un truc ? Ou est-ce le Rudin qui comporte une erreur d'énoncé ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
