Théorème de Darboux

[Anneauprincipal]

Bonjour,

Je dois démontrer le th de Darboux de manière topologique :

On considère f (de R dans R) dérivable, et I un ouvert non vide de R.

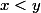
G={ avec , x et y dans I}

Comment démontrer que G est connexe ?

Merci pour vos indications !

[ThSQ]

L'image d'un connexe par une fonction continue est ....



Edit : on en a largement discuté sur le forum il y a peu.