Théorème de Darboux

[legeniedesalpages]

Bonsoir,

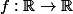
si une fonction vérifie la propriété des valeurs intermédiaires, est-elle dérivable presque partout?

Merci pour vos réponses.

[yos]

Salut.
Ben non : même continue, elle peut n'être dérivable nulle part. Par contre, il me parait plus délicat de savoir si elle admet des primitives.

[Nightmare]

Salut :happy3:

ben non, tu prends une fonction continue partout dérivable nulle part.
Elle vérifie le TVI et pourtant c'est marqué, elle est dérivable nulle part!

[Nightmare]

Un peu long à la détente, salut Yos :happy3:

[legeniedesalpages]

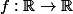
lol non pardon, j'ai fait une coquille, comme dit yos, ce que je voulais savoir, c'est si une fonction vérifie la propriété des valeurs intermédiaires, est-elle la dérivée presque partout d'une fonction?

[Nightmare]

Euh qu'entends-tu par "être la dérivée presque partout d'une fonction" ? En gros coïncider avec la dérivée d'une certaine fonction partout sauf sur un ensemble négligeable?

[legeniedesalpages]

Euh qu'entends-tu par "être la dérivée presque partout d'une fonction" ? En gros coïncider avec la dérivée d'une certaine fonction partout sauf sur un ensemble négligeable?

oui c'est ça.

[ffpower]

On peut trouver des fonctions non mesurables surjectives sur tout intervalle,donc non..

[raito123]

Bonsoir,

Il dit quoi exactement le théorème de Darboux?? :happy2:

[legeniedesalpages]

On peut trouver des fonctions non mesurables surjectives sur tout intervalle,donc non..

Merci,

donc sur tout intervalle I, il existerait une fonction f non mesurable surjective telle que f(IR)=I ? Comment tu les trouves ces fonctions?

[legeniedesalpages]

Bonsoir,

Il dit quoi exactement le théorème de Darboux?? :happy2:

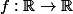
Toute dérivée d'une fonction vérifie le théorème des valeurs intermédiaires.

[raito123]

Ok merci!!

[ThSQ]

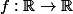
lol non pardon, j'ai fait une coquille, comme dit yos, ce que je voulais savoir, c'est si une fonction vérifie la propriété des valeurs intermédiaires, est-elle la dérivée presque partout d'une fonction?

Je crois pas j'ai vu une fonction qui vérifiait cela et qui n'était continue nulle part. Est-ce qu'une fonction continue nulle part peut être la µ-pp d'une fonction dérivable ? Je crois pas mais je peux me gourer.

[legeniedesalpages]

Je crois pas j'ai vu une fonction qui vérifiait cela et qui n'était continue nulle part. Est-ce qu'une fonction continue nulle part peut être la µ-pp d'une fonction dérivable ? Je crois pas mais je peux me gourer.

c'est quoi cette fonction? :hein:

[yos]

Pour un contrex, il faut davantage que la surjectivité. Il faudrait une fonction qui transforme tout intervalle ouvert en R tout entier. Je crois bien que ça existe.

[Nightmare]

Un lien interressant (fichier PDF)

:happy3:

[ffpower]

je pense que ct la meme que la mienne(non mesurable).mais sinon une fn continue nulle part peut etre une dérivée p-p(ya qu a prendre l indicatrice de Q)
le truc,c est que toute fn continue est egale p-p a une fn continue nulle part^^

[ThSQ]

c'est quoi cette fonction? :hein:

Par exemple : http://en.wikipedia.org/wiki/Conway_base_13_function

Sinon y'a aussi la fonction de Lebesgue qui transforme tout intervalle ouvert non vide en IR complet.

[legeniedesalpages]

ok merci toutes ces informations, je vais me documenter un peu plus avant de poursuivre cette quête. :)