Théorème de convergence dominé de Lebesgue

[joanie58]

Bonjour,

je dois calculer la limite et expliquer s'il est possible de permuter l'intégration et le passage à la limite

[adrien69]

Salut,

C'est faux pour plusieurs raisons.

La pire : 1 n'est pas intégrable sur .

Sinon : première ligne oubli de la valeur absolue (tu ne travailles pas avec des objets positifs !), deuxième et troisième lignes oubli des quantificateurs.

Par contre tu as le bon résultat.

[adrien69]

D'ailleurs il y a bien plus simple que Lebesgue ici (qui est un théorème difficile).



pour

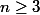
Donc et comme est intégrable sur , on a bien la convergence de ton truc vers 0.

[joanie58]

D'ailleurs il y a bien plus simple que Lebesgue ici (qui est un théorème difficile).

pour

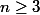
pourquoi ne pas avoir utiliser

pour
pourquoi prendre 3 au lieu de 2 ?

[joanie58]

Salut,

C'est faux pour plusieurs raisons.

La pire : 1 n'est pas intégrable sur .

Sinon : première ligne oubli de la valeur absolue (tu ne travailles pas avec des objets positifs !), deuxième et troisième lignes oubli des quantificateurs.

Par contre tu as le bon résultat.

qu'est-ce que tu veux dire par quantificateurs?

[adrien69]

pourquoi ne pas avoir utiliser

pour
pourquoi prendre 3 au lieu de 2 ?

Parce que n'est pas intégrable en

[joanie58]

Parce que n'est pas intégrable en

mais est-ce que est intégrable en ?

parce que dans le fond pour

donc après je pensais utiliser le théorème de convergence dominer de lebesgue pour interchanger limite et intégrale....

[jlb]

mais est-ce que est intégrable en ?

parce que dans le fond pour

donc après je pensais utiliser le théorème de convergence dominer de lebesgue pour interchanger limite et intégrale....

oui, ce sera bon aussi.