Théorème central limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 12:55
par Dante0 » 25 Déc 2013, 12:55
Bonjour,
D'après le TCL on a :
)
converge vers
)
Comment se fait-il qu'ensuite ce soit équivalent à
}{\sqrt{\sigma^2}})
converge vers
)
?
A ce que je sache

n'est pas égal à 1
Merci !
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 25 Déc 2013, 13:25
par zork » 25 Déc 2013, 13:25
pour moi le TCL c'est ceci:
}{\sqrt{\sigma^2}})
converge vers
)
en loi
tu poses Y une variable aléatoire suivant une loi N(0,1)
en multipliant par

ca donne

et
=\sigma^2V(Y)=\sigma^2)
d'où

suit une loi normale
)
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 15:35
par Dante0 » 25 Déc 2013, 15:35
Mais dans mon exemple comment on passe de
)
à
)
? Normalement on devrait plutot diviser par
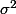
pour que ca donne 1 et non pas par la racine non ? Quel est le "truc" ?
zork a écrit:pour moi le TCL c'est ceci:
}{\sqrt{\sigma^2}})
converge vers
)
en loi
tu poses Y une variable aléatoire suivant une loi N(0,1)
en multipliant par

ca donne

et
=\sigma^2V(Y)=\sigma^2)
d'où

suit une loi normale
)
 = 1)
ici ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 25 Déc 2013, 17:04
par Sylviel » 25 Déc 2013, 17:04
V(Y) = 1 ici ?
Je cite :
Y une variable aléatoire suivant une loi N(0,1)
L'important à se souvenir c'est que la variance c'est "un carré". Donc V(aX)= a²V(X)
et non pas aV(X).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 18:48
par Dante0 » 25 Déc 2013, 18:48
Sylviel a écrit:Je cite :
L'important à se souvenir c'est que la variance c'est "un carré". Donc V(aX)= a²V(X)
et non pas aV(X).
Je pense saisir.
J'en profite pour parler un peu de la variance. Quand on a une expression de la forme
)
Quand on "sort" le 1/n on le met au carré, mais quand on sort la somme c'est juste un "n" qui se retrouve devant normal ? Ce devrait pas être un n² ? (j'ai peut etre déja posé la question, ne me tapez pas dessus ^^)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 25 Déc 2013, 20:05
par zork » 25 Déc 2013, 20:05
si tu sors 1/n ca devient 1/n²
il te reste
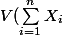= \sum_{i=1}^n V (X_i)+2Cov(X_1,..,X_n))
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 20:09
par Dante0 » 25 Déc 2013, 20:09
zork a écrit:si tu sors 1/n ca devient 1/n²
il te reste
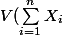= \sum_{i=1}^n V (X_i)+2Cov(X_1,..,X_n))
 = \frac{1}{n^2}nV(X_i) = \frac{\sigma^2}{n})
non ?
Le cas que tu présentes, c'est dans le cas ou la distribution n'est pas iid ?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 25 Déc 2013, 20:41
par zork » 25 Déc 2013, 20:41
si tu es dans le cas iid c'est ce que tu dis. J'ai fais le cas non iid
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 25 Déc 2013, 20:48
par Dante0 » 25 Déc 2013, 20:48
zork a écrit:si tu es dans le cas iid c'est ce que tu dis. J'ai fais le cas non iid
J'ai uniquement appliqué bêtement, mais c'est quoi le concept derrière le fait que la variable soit distribuée iid ou non ?
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 26 Déc 2013, 13:15
par zork » 26 Déc 2013, 13:15
iid signifie: même loi et indépendantes
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 26 Déc 2013, 15:38
par Dante0 » 26 Déc 2013, 15:38
Comment tu arrives au résultat non iid en fait ?
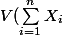= \sum_{i=1}^n V (X_i)+2Cov(X_1,..,X_n))
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 26 Déc 2013, 20:04
par zork » 26 Déc 2013, 20:04
c'est la formule
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
converge vers
en loi
ca donne
suit une loi normale