Theorem central limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 10 Juin 2015, 08:07
par mathelot » 10 Juin 2015, 08:07
bonjour,
le théorème central limite dit que pour une suite infinie
de v.a

i.i.d (indépendantes, identiquement distribuées),
d'espérance

, de variance
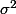
la moyenne

a pour espérance

et pour écart type

la variable centrée réduite

tend en proba vers la loi normale N(0;1)
Auriez vous un exemple de telles suite (X_i) que je vois comment ces propriétés
s'appliquent... ayant un peu de mal de passer de la théorie à la pratique.
merci.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 10 Juin 2015, 08:20
par Monsieur23 » 10 Juin 2015, 08:20
« Je ne suis pas un numéro, je suis un homme libre ! »
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Juin 2015, 08:35
par paquito » 10 Juin 2015, 08:35
Wikipédia, c'est très limité!
-
mathelot
 par mathelot » 10 Juin 2015, 08:43
par mathelot » 10 Juin 2015, 08:43
Est ce qu'on peut applique le TCL
(le théorème central limite) avec la somme

qui a pour espérance

et pour écart type

la variable centrée réduite

tend également en proba (en loi) vers N(0;1)
Qu'est ce qui est le plus fréquent? utiliser

ou
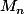
?
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Juin 2015, 09:29
par paquito » 10 Juin 2015, 09:29
mathelot a écrit:Est ce qu'on peut applique le TCL
(le théorème central limite) avec la somme

qui a pour espérance

et pour écart type

la variable centrée réduite

tend également en proba (en loi) vers N(0;1)
Qu'est ce qui est le plus fréquent? utiliser

ou
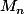
?
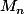
converge en probabilité alors que

est bien approchée par une loi normale, donc tout dépend du contexte. Par exemple, avec une loi U[0; 1[ ,

suit pratiquement une loi N(0; 1) (voir l'expression de la densité dans défi) La loi U[0; 1[ correspond à la fonction random d'une calculatrice (1 est exclus).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
