Théorème de Baire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 23:52
par JackxSummer » 27 Oct 2015, 23:52
MouLou a écrit:Hmm comment tu justifies que l'intersection des Wk est non vide? c'est la qu'il faut les prendre compacts je pense
Il contient au moins le point
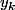
.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 23:58
par MouLou » 27 Oct 2015, 23:58
non, Wk contient y_{k} pour tout k, mais tous les Wk ne contiennent pasun y_{j} qcq
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 28 Oct 2015, 00:11
par JackxSummer » 28 Oct 2015, 00:11
MouLou a écrit:non, Wk contient y_{k} pour tout k, mais tous les Wk ne contiennent pasun y_{j} qcq
Non pas qlq mais

que je choisit pour
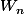
et comme
_k)
est décroissante alors y_n est dans tt les
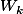
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 28 Oct 2015, 00:15
par MouLou » 28 Oct 2015, 00:15
Justement non... Si la suite etait croissante, alors oui, mais là elle est décroissante, donc t'as aucune garantie que y_{n} reste dans les W_{n+k} pour un n donné
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 28 Oct 2015, 00:25
par JackxSummer » 28 Oct 2015, 00:25
MouLou a écrit:Justement non... Si la suite etait croissante, alors oui, mais là elle est décroissante, donc t'as aucune garantie que y_{n} reste dans les W_{n+k} pour un n donné
Donc, on peut prendre les voisinages fermés ou compacts.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 28 Oct 2015, 00:28
par MouLou » 28 Oct 2015, 00:28
Par hypothèse localement compacte, oui et dans ce cas la tu peux faire les fermés emboités avec ces compacts pour montrer que l'intersection est non vide
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 28 Oct 2015, 00:32
par JackxSummer » 28 Oct 2015, 00:32
MouLou a écrit:Par hypothèse localement compacte, oui et dans ce cas la tu peux faire les fermés emboités avec ces compacts pour montrer que l'intersection est non vide
Dans mon exercice E supposé qlc, pas nécessairement localement compact.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 28 Oct 2015, 00:36
par MouLou » 28 Oct 2015, 00:36
le théorème n'est pas vrai dans le cas général, on sait pas trop quand c'est vrai a part pour localement compact ou metrique complet. Tu voulais une preuve hors complet, je te donne pour localement compact, je peux pas faire mieux
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 28 Oct 2015, 00:41
par JackxSummer » 28 Oct 2015, 00:41
MouLou a écrit:le théorème n'est pas vrai dans le cas général, on sait pas trop quand c'est vrai a part pour localement compact ou metrique complet. Tu voulais une preuve hors complet, je te donne pour localement compact, je peux pas faire mieux
Oh, c'est dommage, Merci bcp :we: .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités