TS2502 a écrit:Bonjour, désolée du retard.
mathelot : J'ai montré plus tôt dans mon exercice que la formule de T-L nous indique qu'il existe c appartenant à ]a;b[ tel que f(b)=f(a)+(b-a)f'(a)+((b-a)²/2)f''(c). Puis dans une autre partie j'ai montré qu'il existe (c
n) entre a et b tel que abs(x
n+1-r) est inférieur ou égal à[(x
n-r)²/2f'(x
n)]abs(f''(c
n))
où abs désigne la valeur absolue et r est le point en lequel f s'annule et étant la limite de (x
n)
pseuda : On cherche à comparer la précision de x
5 issu de la méthode de Newton à la méthode de T-L (donc 6ème terme de la suite). Cependant, je ne vois pas comment les comparer ; l'idée du changement de variable semble correspondre à ce que je souhaite mais je ne vois pas lequel faire : comment passer de sqrt(x+2) à sqrt(X+1) ? En posant X=x+1 ? (sqrt désigne la racine carrée)
Merci de votre aide en tout cas

Bonjour,
En effet, mais je ne vois pas comment faire converger une suite récurrente (définie par
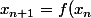))
avec la formule de Taylor de la même façon qu'avec la méthode de Newton. Donc restons sur la formule de Taylor développée à l'ordre 6.
Si je comprends bien (mais j'ai peut-être tout faux), on cherche une valeur approchée de

, avec les moyens du bord (sans calculatrice ni ordinateur). Avec la méthode de Newton et la fonction
=x^2-2)
, cela converge très vite, car
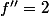
,
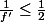
sur l'intervalle [1,2] et l'écart (inférieur à 1 la 1ère fois) est pris au carré à chaque itération.
Avec la formule de Taylor, on cherche à approximer

avec un développement polynomial qu'on sait calculer. On fait le changement de variable sur la fonction
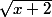
avec
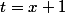
, et on se retrouve à évaluer

à l'aide de la formule de Taylor de la fonction
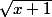
en 0 (qu'on sait calculer) évaluée au point d'abscisse 1, donc à l'ordre 6 et une majoration du reste.



