Système de 3 équations à 3 inconnues avec paramètre
17 messages
- Page 1 sur 1
Système de 3 équations à 3 inconnues avec paramètre
Bonjour, il y a un exercice d'annales que je n'arrive pas à faire.
Résoudre et discuter suivant les valeurs du paramètre m le système :
x+y+(1-m)z = m+2
(1+m)x-y+2z = 0
2x-my+3z = m+2
J'applique le pivot de gauss comme d'habitude.
Je prends le cas m=-2, pour avoir tout = 0, je trouve une infinité de solutions (x,-x,0)
Je prends le cas m différent de -2, et après quelques opérations sur les lignes, j'aboutis au système suivant :
x+y+(1-m)z = m+2
(-m-2)y+(2-(1+m)(1-m))z = -(m+1)(m+2)
(2m-m²)z = m²+2m
dans la 3e équation j'arrive à z = (m+2)/(2-m). Et là je suis bloqué. Je peux écrire le cas m=2 pas de solutions.
Résoudre et discuter suivant les valeurs du paramètre m le système :
x+y+(1-m)z = m+2
(1+m)x-y+2z = 0
2x-my+3z = m+2
J'applique le pivot de gauss comme d'habitude.
Je prends le cas m=-2, pour avoir tout = 0, je trouve une infinité de solutions (x,-x,0)
Je prends le cas m différent de -2, et après quelques opérations sur les lignes, j'aboutis au système suivant :
x+y+(1-m)z = m+2
(-m-2)y+(2-(1+m)(1-m))z = -(m+1)(m+2)
(2m-m²)z = m²+2m
dans la 3e équation j'arrive à z = (m+2)/(2-m). Et là je suis bloqué. Je peux écrire le cas m=2 pas de solutions.
wdbg59 a écrit:Bonjour, il y a un exercice d'annales que je n'arrive pas à faire.
Résoudre et discuter suivant les valeurs du paramètre m le système :
x+y+(1-m)z = m+2
(1+m)x-y+2z = 0
2x-my+3z = m+2
J'applique le pivot de gauss comme d'habitude.
Je prends le cas m=-2, pour avoir tout = 0, je trouve une infinité de solutions (x,-x,0)
Je prends le cas m différent de -2, et après quelques opérations sur les lignes, j'aboutis au système suivant :
x+y+(1-m)z = m+2
(-m-2)y+(2-(1+m)(1-m))z = -(m+1)(m+2)
(2m-m²)z = m²+2m
dans la 3e équation j'arrive à z = (m+2)/(2-m). Et là je suis bloqué. Je peux écrire le cas m=2 pas de solutions.
il manque le cas m=0
et la resolution si le déterminant est non nul
wdbg59 a écrit:ok, j'ai résolu les cas m=0, m=2, m=-2.
J'ai calculé le déterminant, et il est nul pour les valeurs de m =0,2 et -2. Donc en fait, avec un paramètre on doit calculer le déterminant pour trouver les valeurs de m qui nous intéressent ? Ou est-ce juste une coincidence ?
Non on cherche les valeurs de m qui annulent le déterminant dans ce cas le système n'a pas de solution unique
si le déterminant est non nul le système a une solution unique que l'on calcule en fonction de m
sauf erreur on trouve x= -1/(2-m)
y=(m+3)/(2-m) z=(m+2)/(2-m)
ah d'accord. Je trouve également z=(m+2)/(2-m), par contre y et x pas encore. Le problème c'est qu'en remplacant z dans la ligne 2 ca donne de gros calculs quand même, du m^3 ect... Mais bon, je vais quand même essayer.
Donc si j'ai bien compris, avant de faire le pivot de gauss, je calcule le déterminant. Si d=0, pas de solution unique. Si d non nul, alors solution unique pour chaque valeur de m.
Pourtant pour m=0 je trouve une solution unique. Je trouve le triplet (1,1,0). Et en remplacant dans le système, cela marche. Bizarre.
Donc si j'ai bien compris, avant de faire le pivot de gauss, je calcule le déterminant. Si d=0, pas de solution unique. Si d non nul, alors solution unique pour chaque valeur de m.
Pourtant pour m=0 je trouve une solution unique. Je trouve le triplet (1,1,0). Et en remplacant dans le système, cela marche. Bizarre.
salut
je ne vois pas quel est l'intérêt de considérer le cas m = -2 à priori !!
x + y + (1 - m)z = m + 2
(1 + m)x - y + 2z = 0
2x - my + 3z = m + 2
quand j'applique le pivot de Gauss alors la première valeur critique est m = -1 pour se débarrasser des x de la deuxième ligne !!!
m = -1 =>
x + y + 2z = 1
y - 2z = 0
2x + y + 3z = 3
x + 4z = 1
2x + 5z = 3
y = 2z
x + 4z = 1
y = 2z
-3z = 1
...
m <> -1 =>
x + y + (1 - m)z = m - 2
(-2 - m)y + (m^2 + 1)z = -(m + 1)(m + 2)
(-2 - m)y + (2m + 1)z = - 2 - m
la deuxième valeur critique apparaissant est donc m = 2
et ainsi de suite ....
et le calcul du déterminant n'est pas nécessaire !!! par principe du pivot de Gauss ....
je ne vois pas quel est l'intérêt de considérer le cas m = -2 à priori !!
x + y + (1 - m)z = m + 2
(1 + m)x - y + 2z = 0
2x - my + 3z = m + 2
quand j'applique le pivot de Gauss alors la première valeur critique est m = -1 pour se débarrasser des x de la deuxième ligne !!!
m = -1 =>
x + y + 2z = 1
y - 2z = 0
2x + y + 3z = 3
x + 4z = 1
2x + 5z = 3
y = 2z
x + 4z = 1
y = 2z
-3z = 1
...
m <> -1 =>
x + y + (1 - m)z = m - 2
(-2 - m)y + (m^2 + 1)z = -(m + 1)(m + 2)
(-2 - m)y + (2m + 1)z = - 2 - m
la deuxième valeur critique apparaissant est donc m = 2
et ainsi de suite ....
et le calcul du déterminant n'est pas nécessaire !!! par principe du pivot de Gauss ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
le déterminant du système vaut m(m-2)(m+2)
si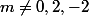 le système admet une solution unique
le système admet une solution unique
qu'on calcule avec, par exemple, le pivot de Gauss
ou un calcul de déterminants.
Les cas m=0 , m=2, m=-2 se traitent à la main en remplaçant
m par sa valeur. Il n'y a pas unicité de la solution,
donc soit une infinité de solution, soit pas de solution du tout.
si
qu'on calcule avec, par exemple, le pivot de Gauss
ou un calcul de déterminants.
Les cas m=0 , m=2, m=-2 se traitent à la main en remplaçant
m par sa valeur. Il n'y a pas unicité de la solution,
donc soit une infinité de solution, soit pas de solution du tout.
oui j'utilise le pivot de Gauss ET le déterminant. Sinon comment trouver les valeurs de m intéressantes ? Je connais pas d'autres méthodes. Après je fais comme l'a dit Mathelot, je remplace chaque m qui annule le déterminant et je fais les pivots de gauss pour chacun des m "intéressant". Après, je fais le pivot avec m quelconque. Dans ton post tu trouves un m=-1, mais -1 n'annule pas le déterminant, donc c'est pour ça que je trouve cette méthode un peu bizarre. Dsl si je ne suis pas compris, je suis pas matheux mais en physique, et moi et l'algèbre ca fait beaucoup.
ok ... mais alors ça n'a pas d'intérêt d'utiliser le pivot de Gauss quand il n'y a plus de paramètres ....
d'autre part il peut apparaître des valeurs critiques qui n'en sont pas : elles apparaissent simplement lorsqu'on applique l'algorithme du pivot de Gauss
ainsi m = -1 ne pose pas de pb pour avoir une solution mais parce qu'il va falloir multiplier par m + 1 qui ne doit pas être nul ...
d'autre part il peut apparaître des valeurs critiques qui n'en sont pas : elles apparaissent simplement lorsqu'on applique l'algorithme du pivot de Gauss
ainsi m = -1 ne pose pas de pb pour avoir une solution mais parce qu'il va falloir multiplier par m + 1 qui ne doit pas être nul ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
ben non cette valeur critique n'en est pas une .... sauf quand on applique l'algorithme du pivot de Gauss
REM : il n'y a pas de cas plus ou moins intéressant qu'un autre ...
il y a trois cas (0, 1 ou un plusieurs solutions) et tout le pb est de savoir dans quel cas on est suivant les valeurs de m ....
REM : il n'y a pas de cas plus ou moins intéressant qu'un autre ...
il y a trois cas (0, 1 ou un plusieurs solutions) et tout le pb est de savoir dans quel cas on est suivant les valeurs de m ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
A mon sens, le petit "détail", c'est qu'on est pas des ordinateurs et donc que l'algo. du pivot de Gauss, on peut essayer de l'appliquer... intelligemment et pas comme un gros bourrin.zygomatique a écrit:ben non cette valeur critique n'en est pas une .... sauf quand on applique l'algorithme du pivot de Gauss
Ca veut dire échanger astucieusement des lignes et/ou ne pas forcément commencer par la première colonne.
En particulier pour les systèmes à paramètres, tant que c'est possible (y compris en faisant des combinaisons linéaires de lignes) on choisi un pivot qui ne dépend pas du paramètre.
Sinon, une remarque pour wdbg59 : dans un exercice où on te demande de déterminer les solutions d'un système à paramètre en fonction du paramètre, tu n'est pas forcément obligé de calculer le déterminant vu que justement, si tu t'y prend pas comme un manche, tout les cas particuliers vont apparaitre naturellement lors de la résolution du "cas général". Par contre, vu le coté chiant des calculs pour résoudre le système, si tu as un peu de rab de temps, le calcul du déterminant est une très bonne vérif. pour voir qu'on s'est pas trop gouré dans les calculs.
Attention à ne pas confondre ce type d'exo. avec ceux où on ne demande pas de déterminer les solutions du systèmes, mais uniquement de déterminer le nombre de solutions du système : là, il est clairement beaucoup plus rapide de commencer par calculer le déterminant du système pour n'avoir à traiter que les "cas particuliers" (pour voir s'il y a une infinité de solutions ou aucune)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
certes oui ... on réfléchit un peu ...
mais quelle que soit la ligne ou la variable il y a un coefficient dépendant de m....
donc que je choisisse x (ou y ... ou z) dans la première ligne (ou une autre) et que je les élimine dans les deux lignes suivantes au moins une combinaison linéaire fera apparaître un coefficient dépendant de m ... et celui-ci ne doit pas être nul ....
maintenant on peut choisir un pivot qui fait que la valeur critique de m l'est finalement effectivement .... mais ça on ne peut pas le savoir avant ... sauf à calculer le déterminant pour connaître ces valeurs critiques ....
dans mon premier post j'ai choisi la variable x et la première ligne qui fait apparaître le coefficient m + 1 et donc la valeur m = -1 qui pose pb ... mais n'est pas un pb ...
j'aurai pu choisir y et faire apparaître la valeur m = 0 qui est effectivement une valeur critique ...
mais je ne peux le savoir à priori ....
mais quelle que soit la ligne ou la variable il y a un coefficient dépendant de m....
donc que je choisisse x (ou y ... ou z) dans la première ligne (ou une autre) et que je les élimine dans les deux lignes suivantes au moins une combinaison linéaire fera apparaître un coefficient dépendant de m ... et celui-ci ne doit pas être nul ....
maintenant on peut choisir un pivot qui fait que la valeur critique de m l'est finalement effectivement .... mais ça on ne peut pas le savoir avant ... sauf à calculer le déterminant pour connaître ces valeurs critiques ....
dans mon premier post j'ai choisi la variable x et la première ligne qui fait apparaître le coefficient m + 1 et donc la valeur m = -1 qui pose pb ... mais n'est pas un pb ...
j'aurai pu choisir y et faire apparaître la valeur m = 0 qui est effectivement une valeur critique ...
mais je ne peux le savoir à priori ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
