Surjectivité d'une fonction

[tom45]

Bonjour,
J'ai à résoudre une question de surjectivité à savoir :
Je dois déterminer l'ensemble des valeurs du paramètres p de R de sorte à ce que la fonction f : R\{1} --> R, définie par f(x) = (x^2 + p)/(x-1) soit surjective.

Pour ce faire j'ai résolu l'équation (x^2 + p)/(x-1) = y, ce qui me donne une équation du second degré x^2 + -yx + (p+y) = 0. Il faut ensuite que le discriminant soit positif ou nul, donc y^2 + 4y - 2p >= 0. Ce qui me permet de trouver p >= -1.

Est-ce correct ?

Merci d'avance

[L.A.]

Bonjour,

la méthode est bonne, l'équation x^2-yx+(p+y)=0 aussi.
Revois ton calcul de discriminant.
Ensuite tu obtiens p <= g(y) et il ne reste plus qu'à trouver le minimum de la fonction g.

[tom45]

Merci pour la réponse. J'ai repris mes calculs :

A partir de x^2-yx+(p+y)=0, le discriminant est (-y)^2 - 4(p+y) = y^2 - 4p - 4y.

Le discriminant étant positif ou nul, on a
y^2 - 4p - 4y >= 0
-4p >= 4y - y^2
p <= -y + (y^2/4)

On étudie alors les variations de la fonction g(y) = -y + (y^2/4).
Je trouve comme minimum -1 atteint en y = 2.

Alors, l'ensemble des valeurs de p tel que la fonction est surjective est p <= -1.

Est-ce que c'est correct ?

[L.A.]

Oui c'est bon

[mathelot]

pour p=-1 pour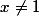

la valeur 2 n'est donc pas une image et f n'est pas surjective si p=-1