Surface de Riemann non compacte, cohomologie

par **Nightmare** » 05 Mar 2009, 00:19

Bonsoir :happy3:

J'aurai juste besoin d'un petit éclaircissement quant à une propriété citée sans démonstration dans un article.

Le contexte est le suivant :

On est dans un espace de Fréchet complexe.

On se fixe une surface de Riemann non compacte quotient d'une surface de Riemann et d'un automorphisme de M d'action libre.

Il est énoncé le résultat suivant :

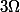il existe une suite de modules différentiels (suite spectrale) convergeant vers la cohomologie de Rham où est le faisceau des germes sur S associé à notre espace de Fréchet

Qu'est-ce qui assure l'existence de cette suite spectrale? Peut-on la décrire?

Merci d'avance.

:happy3:

par **R.C.** » 05 Mar 2009, 10:58

Bonjour,

C'est de l'algèbre homologique méchante... Tu peux regarder ici : http://en.wikipedia.org/wiki/Spectral_sequence
J'ai l'impression que la suite spectrale vient du fait que tu as une filtration sur le complexe associé à ton faisceau (donnée peut-être par une sorte de degré que tu aurais sur ton espace de Fréchet?).

par **Nightmare** » 05 Mar 2009, 14:05

Salut R.C :happy3:

Qu'appelles-tu "degré" ici?

par **R.C.** » 05 Mar 2009, 15:55

Ben en fait au début je pensais que tu travaillais avec le faisceau des formes diff sur S. C'est quoi ton espace de Fréchet : il est quelconque ?

par **Nightmare** » 05 Mar 2009, 16:38

Re salut :happy3:

On sait juste qu'on définie sa topologie par une famille séparante formée de semi-normes !

par **Nightmare** » 05 Mar 2009, 16:48

J'ai pu lire en cherchant un peu que cela relevait de foncteurs dérivés. A priori notre cohomologie de faisceau serait donc construite par une suite de ces foncteurs dérivés

par **barbu23** » 05 Mar 2009, 20:42

Voiçi ce que je trouve pour toi "Nightmare" ! :happy3:
J'espère que ça t'aideras dans tes recherches de reponses :
http://jfviaud.club.fr/node2.html
Il y'a toute une partie consacrée entièrement à la non compacité de la surface de Riemann ! :happy3:
Cordialement ! :happy3:

par **Nightmare** » 05 Mar 2009, 21:38

Merci barbu23 :happy3:

Je vais y jeter un oeil tout de suite !

par **Nightmare** » 05 Mar 2009, 22:30

Ce lien m'aurait bien aidé pour mon exercice précédent (sur les types d'hyperbolicités des surfaces de Riemann) malheureusement il ne m'apporte rien pour cet exercice :(

Merci quand même barbu23 :happy3:

Surface de Riemann non compacte, cohomologie

Surface de Riemann non compacte, cohomologie

Qui est en ligne