Supplémentaire orthogonal
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par TristanTristan » 14 Avr 2009, 13:34
par TristanTristan » 14 Avr 2009, 13:34
Salut à tous, j'ai une question assez précise:
E espace de préhilbertien (dimension quelconque)
F sous-espace vectoriel
Je sais que si F admet un supplémentaire orthogonal, alors (l'othogonal de (l'othogonal de F)) est égal à F,
mais est-ce que la réciproque est vraie?
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 13:45
par emdro » 14 Avr 2009, 13:45
Bonjour,
je ne vois pas trop de quelle réciproque tu parles...
Si c'est: (l'orthogonal de (l'orthogonal de F)) est égal à F => F admet un supplémentaire orthogonal,
alors le problème est réglé puisqu'on présuppose l'existence d'un orthogonal de F...
 par TristanTristan » 14 Avr 2009, 13:50
par TristanTristan » 14 Avr 2009, 13:50
Mais en dimension quelconque, l'orthogonal n'est pas nécessairement un supplémentaire.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 14:05
par emdro » 14 Avr 2009, 14:05
Donc ta question précise est:
si l'orthogonal de l'orthogonal de F est égal à F, F et son orthogonal sont-ils supplémentaires?
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 14:23
par emdro » 14 Avr 2009, 14:23
Maintenant que j'ai compris le problème, il me reste à chercher un peu...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Avr 2009, 14:49
par Nightmare » 14 Avr 2009, 14:49
Salut :happy3:
On a (qu'on soit en dimension finie ou non)
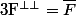
Ainsi si
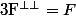
alors F est fermée. Le théorème du supplémentaire orthogonal dans un fermé nous assure donc que
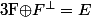
non?
 par TristanTristan » 14 Avr 2009, 14:56
par TristanTristan » 14 Avr 2009, 14:56
Alors moi je suis en prépa, je connais aucun des 2 théorèmes que tu utilises. Mais s'ils sont bons, alors ça marche: F et son orthogonal sont bien supplémentaires dans E.
Merci bien.
 par TristanTristan » 14 Avr 2009, 15:08
par TristanTristan » 14 Avr 2009, 15:08
IL doit y avoir quelques conditions du style: E espace de Hilbert (complet), mais effectivement ça marche.
Merci à tout les deux!
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 15:09
par emdro » 14 Avr 2009, 15:09
Nightmare a écrit:Salut :happy3:
Ainsi si
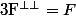
alors F est fermée. Le théorème du supplémentaire orthogonal dans un fermé nous assure donc que
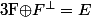
non?
Effectivement, si
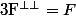
, F est un fermé. On est en bonne voie pour utiliser le théorème du supplémentaire orthogonal, mais ce dernier fonctionne
dans un espace de Hilbert.Il reste à voir le cas où l'espace n'est pas complet...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Avr 2009, 15:27
par Nightmare » 14 Avr 2009, 15:27
effectivement on travaille seulement dans un préhilbertien. A priori sans la complétude il n'y a pas de raison du coup pour que la propriété annoncée soit vraie. Il suffit de trouver un contre exemple du théorème du supplémentaire orthogonal dans le cas où on est dans un espace incomplet.
 par TristanTristan » 14 Avr 2009, 15:36
par TristanTristan » 14 Avr 2009, 15:36
Ne vous embêtez pas, cette réponse me suffit.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 15:39
par emdro » 14 Avr 2009, 15:39
Nightmare a écrit:Il suffit de trouver un contre exemple du théorème du supplémentaire orthogonal dans le cas où on est dans un espace incomplet.
Pas si simple, car l'hypothèse du théorème est:
F fermé
E Hilbert.
or l'hypothèse de Tristan est plus forte:
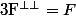
.
En effet, il existe des sous-espaces fermés d'espaces préhilbertiens n'ayant pas de supplémentaire orthogonal.
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 15:39
par emdro » 14 Avr 2009, 15:39
TristanTristan a écrit:Ne vous embêtez pas, cette réponse me suffit.
Ouf :zen: , je nous voyais mal partis!!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 14 Avr 2009, 16:01
par Nightmare » 14 Avr 2009, 16:01
Le problème m'intéresse tout de même, je vais continuer à chercher. Emdro si tu trouves quelque chose fais moi signe :lol3:
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 14 Avr 2009, 17:01
par emdro » 14 Avr 2009, 17:01
Et réciproquement.
Je pense que tu trouveras avant moi: j'ai très peu de temps en ce moment (des copies par dessus la tête et des préparations à n'en plus finir :cry: ).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
alors F est fermée. Le théorème du supplémentaire orthogonal dans un fermé nous assure donc que
non?
