Supplementaire (Algebre)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 11 Fév 2008, 18:15
par Babe » 11 Fév 2008, 18:15
Bonsoir,
j'ai un petit exercice a resoudre:
"Soit V le sous espace vectoriel de R^3 engendré par les vecteurs (1,-1,0) et (1,0,-1)
Trouvez un supplementaire W de V "
Je pense que je dois chercher un sous espace W tel que

mais je ne sais pas comment continuer
merci d'avance

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Fév 2008, 18:28
par nuage » 11 Fév 2008, 18:28
Salut,
il suffit de trouver un vecteur a linéairement indépendant des vecteurs que tu as donné, puis de prendre W=vect(a).
-
trust
- Membre Relatif
- Messages: 163
- Enregistré le: 30 Oct 2007, 20:01
-
 par trust » 11 Fév 2008, 18:29
par trust » 11 Fév 2008, 18:29
il en a beaucoup, suffit de trouver un vecteur libre par rapport aux 2 autres
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 11 Fév 2008, 18:33
par Babe » 11 Fév 2008, 18:33
par exemple je peux prendre a=(0,1,1) car libre
donc W=vect{a} ?

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Fév 2008, 18:56
par nuage » 11 Fév 2008, 18:56
oui, c'est une possibilité. Tu peux aussi prendre a=(0,-100,7) ou a=(0,1,0) ou...
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 11 Fév 2008, 19:02
par Babe » 11 Fév 2008, 19:02
nuage a écrit:oui, c'est une possibilité. Tu peux aussi prendre a=(0,-100,7) ou a=(0,1,0) ou...
oui il y a une infinité de possibilité
quel est l'interet de connaitre les espaces V et W tel que
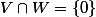
je suppose que c'est utile mais je ne vois pas en quoi
merci

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Fév 2008, 19:10
par nuage » 11 Fév 2008, 19:10
Un des intérêts est :
Si
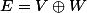
tout vecteur de

s'écrit de façon unique comme somme d'un vecteur de

et d'un vecteur de
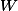
.
Ce qui permet, entre autres, de définir projections et symétries.
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 11 Fév 2008, 19:14
par Babe » 11 Fév 2008, 19:14
ok merci pour ces precisions
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
