Suites et intérêts bancaires

[Baptbe]

Je me sers souvent des suites pour faire des calculs d'intérêts bancaires, mais là je bute !

Mon but était de trouver une formule de récurrence traduisant :

"Je place une somme X à 2,75% par an (arrondi à 0,23% par mois) et tous les mois je fais un nouvel apport de 20€ qui vient s'ajoute à la somme X."

Mon but est de déterminer la somme totale après 5 ans.

S'il n'y avait pas cet apport mensuel de 20€ le problème serait simple : X*(1,0023)^60

Mais avec l'apport je ne trouve pas de formule de récurrence simple...

Le problème peut s'écrire comme U1 = U0 * (1,0023) + 20

J'ai le résultat grâce à l'utilisation d'un tableur mais je souhaiterais trouver le résultat manuellement et en une seule ligne !

Merci.

[Ben314]

Salut,
Tu as donc affaire à une suite de la forme (ici q=1.0023 et r=20) qu'on apelle du poétique nom de "suite arithmético-géométrique".
En math, on résous ça en cherchant une constante k telle que la suite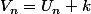 soit purement géométrique, c'est à dire telle que (je te laisse chercher k puis la formule donnant Vn en fonction de n puis celle donant Un en fonction de n : ça te permettra de la retrouver facilement)

Une autre façon de procéder, c'est de faire comme si sur un premier compte tu posait le somme de départ (donc tu calcule dessus des intérêt sur N mensualité) puis, un mois après, tu pose 20 Euros sur un autre compte (donc tu aura des intérêts sur N-1 mensualités) puis un mois plus tard tu recommence avec un 3em compte ... etc
A la fin, tu somme les valeurs de tout les comptes et tu utilise le fait que

[Baptbe]

J'ai posé la suite Vn = Un + C (en calculant C = 20/0,0023 = 8726 ).

Je montre ensuite que Vn est géométrique et je trouve une relation de récurrence sur Un telle que

Un = Vo * (1,0023)^n - C

Je trouve les mêmes résultats que sur mon tableur !

[SAGE63]

[quote="Baptbe"]Je me sers souvent des suites pour faire des calculs d'intérêts bancaires, mais là je bute !

Mon but était de trouver une formule de récurrence traduisant :

"Je place une somme X à 2,75% par an (arrondi à 0,23% par mois) et tous les mois je fais un nouvel apport de 20€ qui vient s'ajoute à la somme X."

Mon but est de déterminer la somme totale après 5 ans.

S'il n'y avait pas cet apport mensuel de 20€ le problème serait simple : X*(1,0023)^60

Mais avec l'apport je ne trouve pas de formule de récurrence simple...

Bonjour,

CAPITAL ACQUIS au BOUT de "n" VERSEMENTS DE FIN DE PERIODE
METHODE DES INTERETS COMPOSES

Pour calculer le capital acquis "Vn" au bout de "n" versements périodiques "a" de fin de période,
au taux périodique "i", on dispose de la formule suivante :

Vn = a * { [ (1+i);) ] - 1 } / i

[chan79]

Je me sers souvent des suites pour faire des calculs d'intérêts bancaires, mais là je bute !

Mon but était de trouver une formule de récurrence traduisant :

"Je place une somme X à 2,75% par an (arrondi à 0,23% par mois) et tous les mois je fais un nouvel apport de 20€ qui vient s'ajoute à la somme X."

Mon but est de déterminer la somme totale après 5 ans.

S'il n'y avait pas cet apport mensuel de 20€ le problème serait simple : X*(1,0023)^60

Mais avec l'apport je ne trouve pas de formule de récurrence simple...

Le problème peut s'écrire comme U1 = U0 * (1,0023) + 20

J'ai le résultat grâce à l'utilisation d'un tableur mais je souhaiterais trouver le résultat manuellement et en une seule ligne !

Merci.

salut
Tu devrais préciser quand les 20 euros sont versés. Est-ce qu'il y a un versement en même temps que la somme X ? Combien de versement de 20 € en tout ?

[mathelot]

bonjour,
il te faut distinguer:

-la période de capitalisation
-les dates d'échéance


La 1ère année donne k_1=(K0+12*20)*1.0275

la seconde
etc....


en général, les intérets générés en moins d'une année ne capitalisent pas
tout au moins dans l'économie légale)


sinon, tu peux même capitaliser "à la seconde" par