Suites de Cauchy

par **mathelot** » 09 Avr 2007, 13:21

Bonjour,

c'est relativement urgent. Comment montre t on qu'une suite à termes réels de Cauchy est convergente ?
je pensais à montrer que:
1) elle est bornée
2) ses suites

et n

sont adjacentes
et leur convergence donne la convergence de

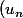Existe il une autre démonstration plus simple ?

par **fahr451** » 09 Avr 2007, 13:28

bonjour

il y a bcp de preuves dont l'une n'en est pas une puisque découle de la construction de R

si on admet le théorème de la borne sup dans R

il y a une preuve élémentaire que j'adore qui est très proche de celle que tu proposes mais compréhensible pour un enfant de 7 ans

par **serge75** » 09 Avr 2007, 13:32

Ca me parait trés raisonnable...
Je réserve toutefois mon avis car tout dépend de la caractérisationde R que tu as. Mais si tu disposes dans ton axiiomatique de R des suites croissantes et majorées, tu dispose alors du critère sur les suites adjacentes et ta preuve tient la route.
Idée d'améliration : pourquoi ne pas considérer que la première de tes deux suites et montrer qu'elle est décroissante et minorée ? ça allègerait un peu.

par **mathelot** » 09 Avr 2007, 13:33

tu peux m'en indiquer les grandes lignes (une démo rigoureuse) ?
mais effectivement, comme les réels sont le quotient des suites de Cauchy par l'idéal des suites de limite nulle, j'ai qu'à prendre ça comme axiome des nombres réels. Ceçi dit, je veux bien un lien avec la propriété de la borne sup.

par **nuage** » 09 Avr 2007, 13:34

Salut,
je dirais que les démonstrations que l'on peut en donner dépendent de la façon dont on a construit

.
Une construction possible étant de rendre toutes les suites de Gauchy convergentes (et dans ce cas iln'y a rein à faire). :zen:

par **abcd22** » 09 Avr 2007, 13:37

Bonjour,
Comme elle est bornee elle a une valeur d'adherence, soit une sous-suite

de

qui converge vers l. Ensuite on ecrit

et comme pour tout n,

, on utilise la definition d'une suite de Cauchy pour montrer que le premier morceau est plus petit que epsilon pour n assez grand.

par **fahr451** » 09 Avr 2007, 13:38

bien sûr c'était provocateur

on ne parle pas de suite de cauchy

tout repose sur le fait qu 'une suite de cauchy qui admet une sous suite convergente converge

on montre 1 qu 'une suite de cauchy est bornée

2 qu 'une suite admet une sous suite monotone

c'est le point 2 qu 'un enfant comprend très bien ( j 'ai testé en vrai)

preuve de 2

on considère une infinité d'hommes qui regardent la mer

lhomme 0 est en premier les autres sont devant lui (faut juste faire admettre à l'enfant que ces hommes sont sans épaisseur)

u(n) est la taille de l 'homme n

il y a deux cas

soit un nbre fini d 'hommes voient la mer -> on construit une sous suite croissante

soit il y a une infinité d'hommes qui voient la mer -> on construit une sous suite décroissante (strictement)

par **mathelot** » 09 Avr 2007, 13:41

au fait, pour changer de sujet sur l'ensemble des nombres réels, je crois me rappeler que Cantor , génial inventeur des cardinaux transfinis, rechignait à
considérer des infiniments petits "actuels". mais à notre époque, il y a une formalisation de la droite numérique autre que les nombres réels classiques avec des infiniments petits "actuels" . c'est l'analyse non-standard, c'est ça ?

merçi à vous pour toutes ces réponses.

Cordialement,

par **serge75** » 09 Avr 2007, 13:43

C'est ça...

par **fahr451** » 09 Avr 2007, 13:45

en tout cas à la même distance du sommet pour tous
ou que la taille est à prendre des pieds aux yeux

Suites de Cauchy

Suites de Cauchy

Qui est en ligne