Suite de sinus a résoudre !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 19:58
par ben_michao » 07 Sep 2006, 19:58
Bonjour a tous ceux susceptible de m'aider sur cet exercice !
l'intitulé se presente ainsi :
"On se propose de calculer la somme :
Sn= sin(a) + sin(2a) + ... + sin(na).
1/Pour quelles valeurs de n cette somme a-t-elle un sens?
2/Ecrire en extension S1 et S2.
3/Rappeler avec la preuve la formule de transformation du produit sin(a)sin(b) en somme.
4/L'utiliser pour transformer le produit P=Sn*sin(a/2).
5/En deduire la valeur de Sn."
Je bloque deja a la premiere question, si vous avez des reponses je suis a votre ecoute.
benjamin
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:02
par nekros » 07 Sep 2006, 20:02
...ce qui ne t'empêche pas de faire les autres :lol4:
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 20:07
par ben_michao » 07 Sep 2006, 20:07
Pourrais tu m'aider sur la premiere question Nekros?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Sep 2006, 20:09
par tize » 07 Sep 2006, 20:09
Elle a un sens pour n'importe quel entier n plus grand ou égal à 1 ...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:20
par nekros » 07 Sep 2006, 20:20
Et les autres questions, tu y arrives ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Sep 2006, 20:28
par tize » 07 Sep 2006, 20:28
nekros a écrit:Et les autres questions, tu y arrives ?
Heu...c'est une question pour moi ou ben_michao ?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:31
par nekros » 07 Sep 2006, 20:31
tize a écrit:Heu...c'est une question pour moi ou ben_michao ?
Pour ben_michao bien sûr :ptdr:
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 20:46
par ben_michao » 07 Sep 2006, 20:46
Non, je me suis arreté pour m'y remettre plus tard mais n'hesitez pas à me donner des reponses, je pourrai verifier ce que je trouve ou m'en inspirer si je bloque, mais j'avoue que la j'ai un peu du mal a avancer...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:48
par nekros » 07 Sep 2006, 20:48
Par exemple pour la 3 (la 2 ya rien à faire), utilise les formes exponentielles pour prouver l'égalité.
a+
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 20:48
par ben_michao » 07 Sep 2006, 20:48
Pensez vous que sin1= sin(a) et que sin2= sin(a) + sin(2a)?
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 20:50
par ben_michao » 07 Sep 2006, 20:50
Effectivememnt la 3 me pose des pb, mais je vais m'y replonger un peu plus tard, merci de votre aide et surtout n'hesiter si vous avez des indices.
merci
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:53
par nekros » 07 Sep 2006, 20:53
ben_michao a écrit:Pensez vous que sin1= sin(a) et que sin2= sin(a) + sin(2a)?
Plutôt
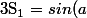)
et
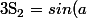+sin(2a))
Tu peux bricoler

:
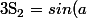+2sin(a)cos(a)=sin(a)(1+2cos(a)))
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:54
par nekros » 07 Sep 2006, 20:54
ben_michao a écrit:Effectivememnt la 3 me pose des pb, mais je vais m'y replonger un peu plus tard, merci de votre aide et surtout n'hesiter si vous avez des indices.
merci
Utilise les formules d'Euler, ça va tout seul :lol4:
a+
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 20:57
par nekros » 07 Sep 2006, 20:57
Oui Mohamed, mais il faut suivre l'exo ...
C'est vrai que ça va plus vite, surtout en utilisant l'angle moitié, mais bon...
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 20:59
par ben_michao » 07 Sep 2006, 20:59
Est ce que si pour la 3/, je dis sin(a)sin(b)=1/2[cos(a-b)-cos(a+b)], je ne reponds pas a la question?
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 21:07
par nekros » 07 Sep 2006, 21:07
Oui, mais on te demande la preuve :
Tu sais que
=\frac{exp{ia}-exp{-ia}}{2i})
, idem avec
)
Donc
sin(b)=\frac{exp{ia}-exp{-ia}}{2i} \times \frac{exp{ib}-exp{-ib}}{2i}=\frac{exp{i(a+b)}-exp{i(a-b)}-exp{-i(a-b)}+exp{-i(a+b)}}{-4}=\frac{2cos(a+b)-2cos(a-b)}{-4}=\frac{1}{2}(cos(a-b)-cos(a+b)))
A+
-
ben_michao
- Membre Naturel
- Messages: 22
- Enregistré le: 07 Sep 2006, 19:45
-
 par ben_michao » 07 Sep 2006, 21:11
par ben_michao » 07 Sep 2006, 21:11
Je trouve ca etonnant d'utiliser Euler pour cet exercice, je ne suis pas censé savoir ces formules pour le resoudre, il doit y avoir une parade
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 21:13
par nekros » 07 Sep 2006, 21:13
ben_michao a écrit:Je trouve ca etonnant d'utiliser Euler pour cet exercice, je ne suis pas censé savoir ces formules pour le resoudre, il doit y avoir une parade
Euler est une parade pour ceux qui ne connaissent pas leurs formules de trigo :ptdr:
Je t'écris la preuve avec que de la trigo
a+
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 21:16
par nekros » 07 Sep 2006, 21:16
On part du membre de gauche :
=cos(a)cos(b)+sin(a)sin(b))
=cos(a)cos(b)-sin(a)sin(b))
Donc
-cos(a+b)=2sin(a)sin(b))
Donc
-cos(a+b))=sin(a)sin(b))
a+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
 ,
,  ........... ,
........... ,  et
et 
 est la somme des termes d'une suite géométrique de terme initial
est la somme des termes d'une suite géométrique de terme initial  et de base
et de base  donc on aurait:
donc on aurait:
)
 pour calculer
pour calculer 
