Exponentiel en sinus par suite

par **tahoser** » 14 Juin 2008, 14:59

De mon côté je cherche à simplifier la somme d'une exponentiel pour montrer qu'on retrouve un sinus.
J'ai donc:

sum_{k=-n/2}^{n/2}=e^{2pi/l k a sin(theta)}
Je voudrais que
sum_{k=-n/2}^{n/2}=sin(pi a n/l sin(theta)) / sin(pi a/l sin(theta))

Et pour ça on passe par:
sin(pi a n/l sin(theta))=(1- e^{2pi/l (n/2 - (-n/2) + 1) a sin(theta)}) / (1- e^{2pi/l a sin(theta)})

Mais du coup y a un soucis mais je vois pas où!

Merci bienDe mon côté je cherche à simplifier la somme d'une exponentiel pour montrer qu'on retrouve un sinus.
J'ai donc:

sum_{k=-n/2}^{n/2}=e^{2pi/l k a sin(theta)}
Je voudrais que
sum_{k=-n/2}^{n/2}=sin(pi a n/l sin(theta)) / sin(pi a/l sin(theta))

Et pour ça on passe par:
sin(pi a n/l sin(theta))=(1- e^{2pi/l (n/2 - (-n/2) + 1) a sin(theta)}) / (1- e^{2pi/l a sin(theta)})

Mais du coup y a un soucis mais je vois pas où!

Merci bien

par **mathelot** » 14 Juin 2008, 15:13

tahoser a écrit:

Faut-il lire p

ou pi=

?

par **tahoser** » 14 Juin 2008, 15:18

Ous c'est (pi * i).
Désolée...

Merci pour le traduc latex par ailleurs

par **mathelot** » 14 Juin 2008, 16:00

le /l c'est une balise ou l'on divise par l'entier l ?

par **tahoser** » 14 Juin 2008, 16:08

On a en fait

par **mathelot** » 14 Juin 2008, 16:33

on pose:

car

par **tahoser** » 14 Juin 2008, 17:47

En fait moi j'utilise pas de partie réelle. J'utilise juste l'équation des suites

Mais je suis pas sûr en fait que ce soit correcte pour l'exponentiel et quel puissance mettre à q quand je vais de -n/2 à n/2

par **mathelot** » 14 Juin 2008, 18:03

tahoser a écrit:En fait moi j'utilise pas de partie réelle.

:triste: :mur:

tu peux scinder la somme en trois, faire un changement d'indice pour les
indices entiers négatifs.

par **tahoser** » 14 Juin 2008, 18:26

Je vois mais du coup ça revient à faire de 0 à N puisque du coup on ferait de 0 à N/2 et de 0 à N/2. Mais du coup si je change le signe pour la première partie (qui serait de -N/2 à 0 normalement), à quoi correspond ce changement dans l'équation?

par **mathelot** » 14 Juin 2008, 18:27

tu es en quel classe ?

par **tahoser** » 14 Juin 2008, 18:49

Disons que ça fait longtemps que j'ai pas refait de tel calcul et que je bloque!

par **mathelot** » 14 Juin 2008, 19:14

bon voilà des formules:

z=x+iy
x=Re(z)
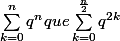
z'=x'+iy'
x'=Re(z')

z+z'=(x+x')+i(y+y')

d'où

re(z+z')=re(z)+re(z')

On peut donc permuter partie réelle et somme.

une somme de cosinus cos(nx) est donc la partie réelle de la somme
des n+1 premiers termes d'une progression
géométrique.

Ta somme est mal écrite, il vaut mieux écrire:

Exponentiel en sinus par suite

Exponentiel en sinus par suite

Qui est en ligne