Suite qui semble géométrique

[titine]

Bonjour,
je recherche une formule :
Sur un cercle on place 2 points, on les relie, le disque est partagé en 2 ;
on place 3 points, on les relie 2 à 2, le disque est partagé en 4 ;
on place 4 points, on les relie 2 à 2, le disque est partagé en 8 ;
on place 5 points, on les relie 2 à 2, le disque est partagé en 16 ; ...
Il semble que la suite soit géométrique, mais non, car le terme suivant est 30.
Je sais que cette formule fait intervenir des combinaisons (bien sûr !) mais je ne m'en sors pas ... !
Pourriez vous m'aider ?
Merci !

[skilveg]

Salut,

Tes points sont sur un polygone régulier ou non? Sinon le nombre de régions dépend de la position des points.

[titine]

Salut,

Tes points sont sur un polygone régulier ou non? Sinon le nombre de régions dépend de la position des points.

Non.
Je cherche le nombre maximal de régions que l'on peut obtenir avec n points quelconques sur le cercle.

[skilveg]

Dans ce cas, pour 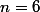il y en a plus que 30: si tu pars d'un hexagone régulier et que tu déplaces un peu un des sommets, tu fais apparaître une nouvelle région au centre.

En admettant que le nombre maximal de régions est obtenu quand trois segments ne se coupent jamais à l'intérieur du disque (avec les mains, dans une telle situation, on décale un peu certains sommets, ce qui supprime l'intersection et crée d'autres régions), on peut donner une formule explicite: on part du cercle (1 région) et on ajoute les segments un par un. Si le segment ajouté ne coupe aucun autre segment à l'intérieur du disque, il ne produit qu'une nouvelle région. Sinon, il rajoute deux régions à chaque intersection. Du coup, comme il y a segments et 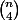intersections possibles à l'intérieur du disque, le nombre de régions à la fin est .

Pour le cas des polygones réguliers, c'est plus compliqué: http://arxiv.org/pdf/math.MG/9508209.

Bonne soirée

[titine]

Merci beaucoup !