Subdivision

[Trident]

Salut, je vous sollicite pour une preuve à compléter où je bloque.



Pour conclure, il faut que je montre que chaque est contenu dans une boule
Ainsi, il suffira de prendre comme subdivision les .

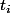
Merci par avance

[Doraki]

En supposant que dans ton recouvrement fini tu n'as pas gardé de boule qui soit complètement incluse dans une autre boule, [ti ; ti+1] est recouvert par la réunion de B(ti,;)i) et de B(ti+1,;)ti+1).

Si ;)i >= ;)i+1 alors ce même intervalle est recouvert par B(ti,2;)i), sur lequel f n'est pas surjective.
Si ;)i <= ;)i+1 alors ce même intervalle est recouvert par B(ti+1,2;)i+1), sur lequel f n'est pas surjective.

[Trident]

Pourquoi justement le passage en gras ?
"Si i >= i+1 alors ce même intervalle est recouvert par B(ti,2;)i), sur lequel f n'est pas surjective."

Question supplémentaire : On est bien d'accord que la réunion de B(ti,;)i) et de B(ti+1,;)ti+1) n'a aucune raison d'être un intervalle ?

[Doraki]

Je suppose que tu as numéroté les xi dans l'ordre croissant (sinon la discussion rime pas à grand chose)

Si les deux boules ne recouvrent pas l'intervalle alors il y a un point x qui n'est pas dans ces boules, c'est à dire qu'il existe x tel que ti + ;)i <= x <= t(i+1) - ;)(i+1).
Ce point x devant être recouvert par une autre boule B(tj,;)j) ; si par exemple tj < ti alors tu peux montrer aisément que ;)j est suffisemment grand pour que B(tj,;)j) contienne entièrement B(ti,;)i).
Donc tu vires ton xi de ton recouvrement et tu recommences tout depuis le début.

Donc maintenant on suppose que t'as pas pris de boule inutile dans ton recouvrement et que tu les as numérotés dans l'ordre croissant. Alors les deux boules ouvertes recouvrent [ti ; t(i+1)].

Je t'en supplie fait un dessin tu vas voir que ce qui suit est complètement trivial.

On en déduit que ;)(i+1) + ;)i > t(i+1) - ti :

Si ti+;)i <= t(i+1) alors comme ti+;)i est dans [ti ; t(i+1)] et n'est pas dans B(ti,;)i), il est forcément dans B(t(i+1),;)(i+1)), et donc t(i+1)- (ti+;)i) < ;)(i+1), c'est à dire ;)(i+1) + ;)i > t(i+1) - ti.
Si ti+;)i > t(i+1) alors on a ;)(i+1) + ;)i > ;)i > t(i+1) - ti.
D'ailleurs dans les 2 cas tu vois que la réunion des 2 boules est un intervalle (puisqe B(ti,;)i) arrive jusqu'à ti+;)i, qui est soit dans l'autre boule, soit derrière t(i+1))

Maintenant si ;)i >= ;)(i+1), alors oui [ti ; t(i+1)] est recouvert par B(ti, 2;)i). Pour ça il suffit de montrer que ti et t(i+1) sont tous les deux dans cette boule.

Bon ti c'est le centre de la boule donc il est dedans.
Ensuite, (t(i+1) - ti) < ;)i+;)(i+1) <= ;)i + ;)i = 2;)i, ce qu'il fallait démontrer.

Ensuite tu fais exactement pareil dans le cas où ;)(i+1) >= ;)i.

[Trident]

Ah je crois avoir compris. En effet, la partie où il faut faire un dessin, c'est trivial.
Ce dont j'avais pas remarqué, c'est qu'il était possible de choisir les ti de sorte que les intervalle se chevauchent.
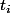
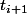
Donc en prenant et au hasard dans notre subdivision , soit les intervalles se chevauchent et donc on les garde dans la subdivision, soient ils se chevauchent pas et alors :


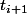
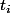
On regarde . Il est dans un certain Si , on vire et on garde , on travaillera donc avec


Mais si on est dans un situation comme celle ci :



Faut recommencer le même raisonnement avec tj+;)j et tk-;)k et dire que ça va se chevaucher à un moment donné car les ti sont finis?

[Trident]

En fait, c'est tout con cet exercic, j'ai compris, c'est bon.
Merci doraki

[Doraki]

oui à chaque fois que tu trouves un "trou" tu peux enlever à coup sûr une de tes boules. Comme tu en as un nombre fini au départ, tu ne peux pas continuer comme ça indéfiniment.

[Trident]

Dernière question pour être sûr. La possibilité suivante est elle possible ?


Elle ne présenterait aucun problème car alors il faudrait virer ti et ti+1 et donc remplacer ti par tj et ti+1 par tk.
Mais pour être sûr de pas écrire des bêtises, la situation est envisageable ?

[Ben314]

Salut,
Normalement, tout est parfaitement envisageable (pourvu que ça recouvre ce qui est bien le cas ici).
Sauf que, si tu veut pas te faire c..., tu commence par dire que, non seulement tu peut extraire un sous recouvrement fini (grâce à la compacité) mais aussi en prendre un où le nombre d'élément du recouvrement est le plus petit possible (grâce au fait que tout ensemble non vide d'entiers naturels admet un plus petit élément).
Avec ça, tu est sûr que dans ton recouvrement, il n'y aura pas un des intervalle qui en contient un autre et ça va t'éviter des discutions oiseuses.

[Trident]

Salut,
Normalement, tout est parfaitement envisageable (pourvu que ça recouvre ce qui est bien le cas ici).
Sauf que, si tu veut pas te faire c..., tu commence par dire que, non seulement tu peut extraire un sous recouvrement fini (grâce à la compacité) mais aussi en prendre un où le nombre d'élément du recouvrement est le plus petit possible (grâce au fait que tout ensemble non vide d'entiers naturels admet un plus petit élément).
Avec ça, tu est sûr que dans ton recouvrement, il n'y aura pas un des intervalle qui en contient un autre et ça va t'éviter des discutions oiseuses.

En effet, du coup ça allège considérablement ma rédaction, merci!