Analyse : subdivision pointée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 14 Avr 2016, 14:06
par Etonnai » 14 Avr 2016, 14:06
Bonjour, tout d'abord merci d'avance pour toute éventuelle aide apportée pour la résolution de mon exercice.
J'ai donc cet exercice concernant les subdivisions pointées à résoudre. Je bloque pour sa résolution, en voici l'énoncé :
Soiti f : [a,b] -> R de classe C1. On pose 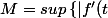 \right| ; t\in [a,b]\right\})
(1) Montrer que si u, v 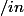 [a,b] et u < v, alors
[a,b] et u < v, alors
-f(u) \right|dt}\leq M\frac{(v-u)^{2}}{2})
(2) En déduire que pour toute subdivision pointée S = ,...,(J_{N-1},t_{N-1}))) de [a,b] on a :
de [a,b] on a :
-\int_{a}^{b}{f(t)dt} \right|\leq \frac{M}{2}\sum_{k=0}^{N-1}{\left|J_{k} \right|^{2}})
(3) Conclure que pour tout n  N*, on a :
N*, on a :
-\int_{a}^{b}{f(t)dt} \right|\leq M\frac{(b-a)^{2}}{2n})
Le trait est en dessous du S ce n'est pas une barre de fraction, mais représente la Subdivision pointée inférieurOù j'en suis :
De l'énoncé je peux dire que f est dérivable et que f'(t) est une fonction continue sur [a,b]. De plus on a :
M
 \right|)
pour t

[a,b].
Pour la question (1) : u,v

[a,b] et u < v -> 0<v-u -> f'(t)<M(v-u) voilà où j'en suis je viens de recommencer l'analyse je galère un peu à démarrer l'exercice un coup de pouce serait le bienvenue, merci!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Avr 2016, 15:04
par Ben314 » 14 Avr 2016, 15:04
Etonnai a écrit:(1) : u,v

[a,b] et u < v -> 0<v-u ->
f'(t)<M(v-u)
???????
Je vois vraiment pas comment tu fait pour "passer" de |f'(t)|<=M pour tout t à f'(t)<=M(v-u) : il sort d'où le v-u là dedans ?
Par contre le théorème des accroissement finis te dit immédiatement que, si |f'(t)|<=M pour tout t d'un l'intervalle I, alors pour tout u,v de I, on a |f(v)-f(u)|<=M.|v-u| (i.e. si la vitesse instantanée est en permanence majorée par M alors la distance_parcourue <= M . temps_de_parcours)
Et c'est clairement ça qu'il faut que tu utilise içi.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 14 Avr 2016, 15:26
par Etonnai » 14 Avr 2016, 15:26
Dur la reprise, comment j'ai pu écrire cette bourde..
Donc oui je venais de revoir dans mon cours le théorème des accroissement finis.
Pour la suite après les accroissements finis, je ne vois pas comment arrivé au résultat, je n'applique pas l'intégrale des deux côtés ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Avr 2016, 16:04
par Ben314 » 14 Avr 2016, 16:04
C'est bien ça : tu écrit que, pour tout t de [u,v], tu as |f(t)-f(u)|<=M|t-u|=M(t-u) et tu intègre pour t variant de u à v.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 14 Avr 2016, 16:18
par Etonnai » 14 Avr 2016, 16:18
D'accord donc j'obtiens :
-f(u) \right|}\leq \int_{u}^{v}{M(t-u)}=[Mt^{2}-Mut])
(de u à v)
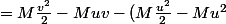=M\frac{v^{2}}{2}-Muv=M(\frac{v^{2}}{2}-uv)=M(\frac{v^{2}-2uv}{2}))
J'ai du faire une erreur quelque part je n'arrive pas à voir où ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Avr 2016, 17:52
par zygomatique » 14 Avr 2016, 17:52
salut
une primitive de t -- > M(t - u) est t -->
^2)
une primitive de t --> M(t - u) est t -->
)
quelle est la différence entre les deux ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Avr 2016, 19:03
par Ben314 » 14 Avr 2016, 19:03
Et je complèterais en disant que, par contre, t -->
 n'est pas
n'est pas une primitive de t -- > M(t - u) ...
Et de toute façon, pour u<v fixés, la droite d'équation y=x-u, c'est clairement la diagonale du carré [u,v]x[0,v-u] donc la "surface sous la courbe", ben c'est la moitié de la surface du carré épicétou...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 14 Avr 2016, 19:44
par Etonnai » 14 Avr 2016, 19:44
Merci beaucoup à vous deux! J'ai maintenant réussi à terminer la question (1).
Pour la
Question (2) j'ai dans mon cours cette définition :
Soit f [a,b] -> R. Pour toute subdivision S =
,...,(J_{N-1},t_{N-1})))
de [a,b], on pose :
=\sum_{k=0}^{N-1}{f(t_{k})\left|J_{k} \right|})
avec

qui représente la longueur de Jk
Je ne vois pas trop par quelle méthode je peux arrivé au résultat de la question (2), merci de m'éclairer..

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Avr 2016, 22:38
par Ben314 » 14 Avr 2016, 22:38
Si

alors
dt=\sum_{k=0}^{N-1}\int_{u_k}^{v_k}f(t)dt)
et donc
-\int_{a}^{b}f(t)dt|=\left|\sum_{k=0}^{N-1}\Big(\int_{u_k}^{v_k}f(t)dt-(v_k\!-\!u_k)f(t_k)\Big)\right|)
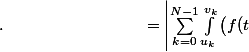-f(t_k)\big)dt\right|)
-f(t_k)\big|dt)
Et tu majore en faisant comme à la question 1).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 16 Avr 2016, 11:34
par Etonnai » 16 Avr 2016, 11:34
Merci beaucoup pour ton aide Ben, j'ai terminé la question 2, il fallait penser à la petite astuce de réutiliser la question 1).
Pour ce qui est de la question 3) Comme on remplace S par Sn je ne sais pas comment commencer je me doute que je vais devoir réutiliser les questions précédentes, mais comment démarrer, car je ne sais pas par quoi majorée ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Avr 2016, 17:13
par Ben314 » 16 Avr 2016, 17:13
Je sais pas ce que c'est que "la subdivision pointée inférieure" (je crois pas avoir jamais entendu parler de ça).
Mais vu le résultat, je parierais très fort qu'on a coupé l'intervalle [a,b] en n sous intervalles de même longueur et donc que les |Jk| de la question 2) valent tous (b-a)/n.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 16 Avr 2016, 17:20
par Etonnai » 16 Avr 2016, 17:20
Bonjour Ben,
Je pense que tu as raison! J'ai inventer le nom je pense car nous ne l'avons jamais nommé clairement dans mon cours.
Dans le cours nous avons écrit : On dit que R(f,S) est la somme de Riemann pour f associé à la subdivision pointée S. Cas des subdivisions régulières.
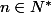
=\frac{(b-a)}{n}\sum_{b=a}^{n-1}{f(a+k\frac{(b-a)}{n})})
-
Etonnai
- Membre Naturel
- Messages: 60
- Enregistré le: 31 Jan 2016, 15:06
-
 par Etonnai » 16 Avr 2016, 18:28
par Etonnai » 16 Avr 2016, 18:28
Merci encore à toi Ben et aussi à Zygomatique pour la résolution de mon exercice. Je l'ai terminé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
