Stat-proba: Ordre...stochastique dans les idées!!!

[Tlanne]

Beh voilà j'ai ce problème:
Soit X une v.a. de support inclus dans [a,b], de moyenne µ et de variance s^2 (^ symbole de l'élevation à la puissance). Considérons la v.a. Xmax de fonction de survie ou de qeue 1-Fmax(x)=P(Xmax > x),
P(Xmax > x) = 1 si x x) = µ/x si µ x) = 1/[1+((x-µ)/s)^2] si x > µ+(s^2)/µ

Montrer que X <= st Xmax (où <= st désigne l'ordre stochastique; il est quelque fois noté <= 1 pour dominance stochastique d'ordre 1)

[BQss]

Salut,

je ne vois pas en ce qui me concerne l'interet de rajouter l'ordre "stochastique" vu qu'on parle déja de variable aléatoire c'est implicite, je ne l'ai jamais vu.

[BQss]

Ensuite il te faut montrer que
C'est à dire:
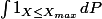=1

PS: avec la definition que j'ai comprise d'ordre stochastique on ne trouve pas 1.
Quelle est donc la definition d'ordre stochastique?

*edit: j'ai trouvé sur internet(si tu nous rapporte pas la definition difficile de t'aider...) On dit que la loi P est stochastiquement inferieur a la loi P' si (attention à l'ordre).
Ce qui donne aussi en "inversant"...

il ne te reste donc qu'a comparer tes fonctions de repartitions ou fonction de survies, c'est pas bien difficile, tu as essayé de le faire avant de nous demander :marteau: :zen: ?

[Isomorphisme]

Bonjour,

N'as-tu pas d'hypothèse sur la densité de ?
La dominance stochastique d'ordre 2 est vérifiée, mais ce n'est qu'une condition nécessaire à la dominance stochastique d'ordre 1 !!

[BQss]

Deja la definition ne colle pas:
"P(Xmax > x) = 1 si x >= µ"

Je suppose que ici c'est plutot

Ce qui indique que le support de est

Pour le probleme est donc reglé car on a bien la fonction de survie de X max qui est superieur à celle de X.

[BQss]

Ensuite par exemple pour µ x)=\frac{E(X)}{x}=\int_a^bf(t)\frac{t}{x}dt[/TEX]


et

avec f la densité de X

[Tlanne]

Définition ordre stochastique :Soit W une v.a. de fonction de répartion FW et Z une v.a. de fonction répartition FZ.
On dit que la loi de W majore strictement pour l'ordre stochastique la loi Z, si
FW(t) <= FZ(t) pour tout t réel, avec inégalité stricte pour au moins une valeur de t.
On le note alors Z <=st W

Ensuite il te faut montrer que
C'est à dire:
=1

PS: avec la definition que j'ai comprise d'ordre stochastique on ne trouve pas 1.
Quelle est donc la definition d'ordre stochastique?

*edit: j'ai trouvé sur internet(si tu nous rapporte pas la definition difficile de t'aider...) On dit que la loi P est stochastiquement inferieur a la loi P' si (attention à l'ordre).
Ce qui donne aussi en "inversant"...

il ne te reste donc qu'a comparer tes fonctions de repartitions ou fonction de survies, c'est pas bien difficile, tu as essayé de le faire avant de nous demander :marteau: :zen: ?

[Tlanne]

Je pense que pour ce cas, on pourrait aussi appliquer l'inégalité de Markov ==> P(X > x) µ+(s^2)/µ , je flaire l'inégalité de Bienaymé Tchébichev mais j'arrive pas à percer le tuyaux.... J'ai assez travaillé Markov aussi pour ce dernier cas; il pourrait marcher car il faut savoir borner µ/x de sorte à trouver l'inégalité recherchée :hein:

Ensuite par exemple pour µ x)=\frac{E(X)}{x}=\int_a^bf(t)\frac{t}{x}dt[/TEX]


et

avec f la densité de X

[BQss]

Je pense que pour ce cas, on pourrait aussi appliquer l'inégalité de Markov ==> P(X > x) µ+(s^2)/µ , je flaire l'inégalité de Bienaymé Tchébichev mais j'arrive pas à percer le tuyaux.... J'ai assez travaillé Markov aussi pour ce dernier cas; il pourrait marcher car il faut savoir borner µ/x de sorte à trouver l'inégalité recherchée :hein:

Tout a fait Markov, très bonne idée et alors pourquoi tu n'y arrives pas après?
si µ t)[/TEX]

Il ne te reste donc plus qu'a traiter le cas si x > µ+(s^2)/µ...

Il faut montrer que sur {x > µ+(s^2)/µ}
c'est a dire que tu dois montrer que sur {x > µ+(s^2)/µ}:
(2) a ce moment là tu appliques Bienaymé Tchébichev et tu obtiens
et donc


La seule difficulté c'est de demontrer (2), ce n'est peut-etre pas faisable en vertu des hypothèse de l'exo, si ca marche pas essaie de majorer autrement(c'est vrai que cette partie est plus délicate).

PS: j'ai parfois employé E(X) parfois fais attention.

[Tlanne]

Salut,
J'ai parfaitement appliqué Markov; suis le sens de mon implication (==>) dans le post précedent.
Je câlais pour le dernier cas où je disais que je flairais Bienaymé.
Je vais creuser ton idée pour son utilisation..

Tout a fait Markov, très bonne idée et alors pourquoi tu n'y arrives pas après?
si µ t)[/TEX]

Il ne te reste donc plus qu'a traiter le cas si x > µ+(s^2)/µ...

Il faut montrer que sur {x > µ+(s^2)/µ}
c'est a dire que tu dois montrer que sur {x > µ+(s^2)/µ}:
(2) a ce moment là tu appliques Bienaymé Tchébichev et tu obtiens
et donc


La seule difficulté c'est de demontrer (2), ce n'est peut-etre pas faisable en vertu des hypothèse de l'exo, si ca marche pas essaie de majorer autrement(c'est vrai que cette partie est plus délicate).

PS: j'ai parfois employé E(X) parfois fais attention.

[Tlanne]

Bonjour Isomorphisme
Je ne preçois pas bien la relation entre les dominations stoch d'ordre 1 et 2; aussi, peut tu m'indiquer comme établir la dominance stoch d'ordre 2 même si c'est une CN pour l'ordre 1.
Merci.

Bonjour,

N'as-tu pas d'hypothèse sur la densité de ?
La dominance stochastique d'ordre 2 est vérifiée, mais ce n'est qu'une condition nécessaire à la dominance stochastique d'ordre 1 !!