Salut,
Si vraiment y'a besoin d'une confirmation, ben je confirme que, effectivement, partant de
=\sqrt{n}-\dfrac{1}{2}+o(1))
qui est une vrai égalité et pas un équivalent (*) tu as tout a fait le droit d'en déduire que
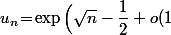\Big))
c'est à dire que
}{\exp(\frac12)}\!\times\!\exp(o(1)))
.
Et comme
))
tend vers
\!=\!1)
cette dernière égalité signifie en fait que
}{\exp(\frac12)})
.
(*) Et là où c'est bien clair que c'est pas "de la composition d'équivalent" qu'on fait, c'est que si on te demandait uniquement
un équivalent de
)
, tu pourrait donner uniquement le
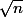
vu que le

ne sert à rien en terme d'équivalent (i.e.

) alors qu'une fois qu'on prend l'exponentielle, le

devient indispensable (i.e.
}{\exp(\frac12)}) n'est pas
n'est pas équivalent à
)
.
Sinon, concernant le "quand on cherche un équivalent, il doit être de quelle forme ?", ben y'a pas bien de réponse à part "le plus simple possible".
Si y'a un équivalent de la forme
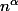
, tant mieux (vu que c'est très simple), mais par exemple
\big)}{\pi\!\times\!\ln(\ln(\ln(n)))})
, il est équivalent à... rien de plus simple que lui même...
