Bonjour à tous,
Je veux essayer de montrer que si un sous groupe est spécial, il est normal.
Définition (C'est pour les notations que je vais utilisée) : Un sous-groupe H d’un groupe G est appelé spécial si, pour toute paire d’éléments x,y ∈ G avec x qui n'appartient pas à H, il existe un unique u ∈ H tel que yx y^−1 = ux u^−1
J'ai procédé ainsi :
Je prends y∈H, j'ai alors yx y^(−1) = ux u^(−1) <=> x y^(-1) u = y^(-1) u x <=> xH=Hx (*)
Mon problème est que (*) est vrai que pour x qui n'est pas dans H mais pour que ce soit normal, il faut que ce soit vrai pour tout x ∈ G.
Je mets la résolution du prof que j'ai pas trop compris. Je préfère trouver une solution pour compléter mon début de démonstration.
Merci
Un sous groupe spécial est normal (BA2)
8 messages
- Page 1 sur 1
Re: un sous groupe spécial est normal (BA2)
Bonsoir,
Hum, je ne comprends pas ta dernière équivalence (avec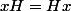 ). Tu oublies de quantifier, ce qui fait que ton "raisonnement" ne tient pas la route.
). Tu oublies de quantifier, ce qui fait que ton "raisonnement" ne tient pas la route.
Moi, je procéderais ainsi : prendre un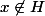 , et montrer qu'on ne peut pas avoir de conjugué de
, et montrer qu'on ne peut pas avoir de conjugué de  dans
dans  .
.
Hum, je ne comprends pas ta dernière équivalence (avec
Moi, je procéderais ainsi : prendre un
Re: un sous groupe spécial est normal (BA2)
Bonjour, merci pour votre réponse.
Ma dernière équivalence vient du fait que j'ai pris y dans H donc y^(-1)x est également dans H. Donc conjugué un élément de H par x revient à obtenir un élément de H. Donc xHx^(-1) = H, je peux aussi dire xH=Hx.
Ceci arriverait à prouver que H est normal si x était quelconque dans G mais ce n'est pas le cas.
Dans votre raisonnement, je ne comprends pas en quoi montrer qu'on ne peut avoir de conjugué de x dans H montre que H est normal.
S'il vous plait, si vous voulez encore m'accorder de votre temps.
Ma dernière équivalence vient du fait que j'ai pris y dans H donc y^(-1)x est également dans H. Donc conjugué un élément de H par x revient à obtenir un élément de H. Donc xHx^(-1) = H, je peux aussi dire xH=Hx.
Ceci arriverait à prouver que H est normal si x était quelconque dans G mais ce n'est pas le cas.
Dans votre raisonnement, je ne comprends pas en quoi montrer qu'on ne peut avoir de conjugué de x dans H montre que H est normal.
S'il vous plait, si vous voulez encore m'accorder de votre temps.
Re: un sous groupe spécial est normal (BA2)
Salut,
Or dans ta prose, je ne vois rien qui montre que ton "t" est un élément QUELQUONQUE de G.
GaBuZoMeu t'a déjà dit que le problème c'est que tu ne quantifie rien du tout : Pour montrer que H est normal, il faut montrer que, POUR TOUT y de H et POUR TOUT t de G, l'element tyt^(-1) est dans H.Siham a écrit:Ma dernière équivalence vient du fait que j'ai pris y dans H donc y^(-1)x est également dans H. Donc conjugué un élément de H par x revient à obtenir un élément de H.
Or dans ta prose, je ne vois rien qui montre que ton "t" est un élément QUELQUONQUE de G.
Modifié en dernier par Ben314 le 08 Aoû 2022, 17:17, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un sous groupe spécial est normal (BA2)
Bonjour Ben314, merci pour votre réponse.
Je suis vraiment désolée mais je sais cela et c'est justement le soucis que j'essaye de résoudre.
Comment faire pour que x plus haut et t chez vous soit quelconque ?
Je suis vraiment désolée mais je sais cela et c'est justement le soucis que j'essaye de résoudre.
Comment faire pour que x plus haut et t chez vous soit quelconque ?
Re: un sous groupe spécial est normal (BA2)
Le problème est de faire un raisonnement correct, en quantifiant tout précisément.
Je t'ai déjà suggéré une piste :
Prendre un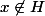 et montrer qu'il n'a aucun conjugué dans
et montrer qu'il n'a aucun conjugué dans  . On raisonne par l'absurde : supposons qu'il existe
. On raisonne par l'absurde : supposons qu'il existe 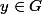 tel que
tel que 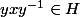 . Je te laisse poursuivre pour arriver à une absurdité, et comprendre pourquoi ça entraîne bien que
. Je te laisse poursuivre pour arriver à une absurdité, et comprendre pourquoi ça entraîne bien que  est normal.
est normal.
(Ben314 a fait un lapsus : il faut lire dans son message "POUR TOUT y de H et POUR TOUT t de G, l'element tyt^(-1) est dans H.")
Je t'ai déjà suggéré une piste :
Prendre un
(Ben314 a fait un lapsus : il faut lire dans son message "POUR TOUT y de H et POUR TOUT t de G, l'element tyt^(-1) est dans H.")
Re: un sous groupe spécial est normal (BA2)
J'ai corrigé l'erreur du post précédent.
Merci.
Merci.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: un sous groupe spécial est normal (BA2)
Bonjour, pour la démo par l'absurde j'ai ceci :
On suppose qu'il existe un y dans G yxy^(-1) est dans H. Il existe alors un u dans H tq yxy^(-1) = uxu^(-1) car H est spécial.
yxy^(-1)=uxu^(-1) <=> x = [y^(-1)u] x [y^(-1)u] ^(-1)
On a supposé par l'absurde que les conjugués de x sont H donc par égalité ceci veut dire que x est dans H. CONTRADICTION
Donc x n'as pas de conjugué dans H.
J'espère qu'il n'y a pas d'erreur.
Par contre j'ai toujours pas trouvé pourquoi ceci montre que H est normal.
On suppose qu'il existe un y dans G yxy^(-1) est dans H. Il existe alors un u dans H tq yxy^(-1) = uxu^(-1) car H est spécial.
yxy^(-1)=uxu^(-1) <=> x = [y^(-1)u] x [y^(-1)u] ^(-1)
On a supposé par l'absurde que les conjugués de x sont H donc par égalité ceci veut dire que x est dans H. CONTRADICTION
Donc x n'as pas de conjugué dans H.
J'espère qu'il n'y a pas d'erreur.
Par contre j'ai toujours pas trouvé pourquoi ceci montre que H est normal.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 119 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
