Sous-groupe additif de R

[Zweig]

Salut,

J'ai un peu de mal avec les exercices impliquant les bornes sup/inf ...

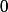
On considère une partie de non réduite à et vérifiant la propriété suivante :



On considère

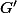
a) Montrer que admet une borne inférieure, notée .

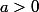
b) On suppose . Montrer que

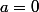
c) Montrer que si , alors est dense dans .

Pour la a), clairement G' est non vide (on montre qu'il contient forcément un réel positif). Après faut montrer que G' est borné ... Mias par quoi ?

Pour les autres questions, je bloque aussi ...

Merci d'avance ! :marteau:

[girdav]

Salut.
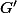
Il me semble qu'il suffit que soit minoré et non pas borné.

[Nightmare]

Salut !

On intersecte G avec ]0,+oo[ justement pour obtenir un ensemble minoré (par 0) qui admet donc une borne inférieure. Ce raisonnement est très employé.

[Zweig]

Désolé, je voulais dire minoré ! Donc il suffit juste de dire comme R+* est minoré, alors G' est minoré ?

Des pistes pour les autres ?

[Nightmare]

Eh bien oui, puisqu'en particulier les éléments de G' sont dans R+* donc minorés par 0 !

Pour la 2) prends y dans G qui n'est pas dans xZ et effectue la division de y par x !