Sous-espace fermé et projection orthogonale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 02 Avr 2008, 17:47
par legeniedesalpages » 02 Avr 2008, 17:47
Bonsoir,
je bloque sur cet exercice:
1) Pour chaque entier

on note
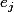
l'élément de
)
défini par
[CENTER]
=1)
si
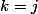
et
=0)
si
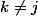
. [/CENTER]
La famille
_{j\in \mathbb{N}})
est-elle une base orthonormale de
,(.|.)_{\textrm{can}}))
?
2) Pour chaque entier

on note

. Justifier que V_j est un \mathbb{K}-sous-espace vectoriel fermé de
(\mathbb{N}))
et décrire la projection orthogonale

sur

.
Pour la 1), c'est ok, mais pour la 2) je bloque pour montrer que

est un sous-espace
fermé de
)
.
Merci pour votre aide.
 par alavacommejetepousse » 02 Avr 2008, 17:48
par alavacommejetepousse » 02 Avr 2008, 17:48
bonsoir
que dire d'un espace vectoriel de dimension finie ?
 par legeniedesalpages » 02 Avr 2008, 17:51
par legeniedesalpages » 02 Avr 2008, 17:51
alavacommejetepousse a écrit:bonsoir
que dire d'un espace vectoriel de dimension finie ?
il est complet car produit fini du corps qui l'est aussi.
 par alavacommejetepousse » 02 Avr 2008, 17:52
par alavacommejetepousse » 02 Avr 2008, 17:52
oui donc facile de voir qu 'un sev de dim finie est fermé
 par legeniedesalpages » 02 Avr 2008, 17:56
par legeniedesalpages » 02 Avr 2008, 17:56
alavacommejetepousse a écrit:oui donc facile de voir qu 'un sev de dim finie est fermé
oui c'est vrai question bête :marteau:
merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités