Sommes (Équivalence a linfinie) [Image corrigée]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ayalisa
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Nov 2015, 21:18
-
 par ayalisa » 18 Nov 2015, 14:28
par ayalisa » 18 Nov 2015, 14:28
Coco mes chers matheux :party: :party:
1/

(équivalence en +oo)
Pour cette equivalence si on fait diviser la somme par le terme a droite , on aura bien : 1+quq chose
cette "quq chose" est (1/e^(2n-1) +...+1/e^(n^2)) qui est clair qu'elle tend vers 0 , pour moi c'est clair mais comment le démontrer ?
2/Image corrigée
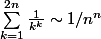
(équivalence en +oo)
Pour cette équivalence , si on divise la somme par le terme a droite , on aura de meme , 1+la somme(donnée) de k= n+1 jusqu'a 2n , je n'arrive pas a démonter que ce terme tend vers 0
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 18 Nov 2015, 17:00
par Kolis » 18 Nov 2015, 17:00
ayalisa a écrit:Coco mes chers matheux :party: :party:
1/

(équivalence en +oo)
Pour cette equivalence si on fait diviser la somme par le terme a droite , on aura bien : 1+quq chose
cette "quq chose" est (1/e^(2n-1) +...+1/e^(n^2)) qui est clair qu'elle tend vers 0 , pour moi c'est clair mais comment le démontrer ?
Majores chaque terme de la somme par le plus grand, il y a

termes et une limite facile à trouver.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 18 Nov 2015, 17:04
par Kolis » 18 Nov 2015, 17:04
Pour le 2. je ne vois pas du tout d'où tu sors le 1+... !
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Nov 2015, 17:37
par aymanemaysae » 18 Nov 2015, 17:37
Pour la question n° 1:
on a sum(k=0 à n){exp(k^2)} => exp(n^2), ceci d'une part, et d'autre part on a:
0<= k <= n <--> 0<= k^2 <= kn <--> exp(k^2) <= exp(kn) .
A partir de là, vous pouvez continuer pour encadrer sum(k=0 à n){exp(k^2)} et conclure.
Bon courage.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 18 Nov 2015, 18:13
par aymanemaysae » 18 Nov 2015, 18:13
Pour la question n° 2 : est ce bien 1/n^n ?
-
ayalisa
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Nov 2015, 21:18
-
 par ayalisa » 19 Nov 2015, 00:22
par ayalisa » 19 Nov 2015, 00:22
aymanemaysae a écrit:Pour la question n° 2 : est ce bien 1/n^n ?
Image corrigée
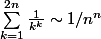
je m'excuse , voila corrigée
-
ayalisa
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Nov 2015, 21:18
-
 par ayalisa » 19 Nov 2015, 00:24
par ayalisa » 19 Nov 2015, 00:24
Kolis a écrit:Pour le 2. je ne vois pas du tout d'où tu sors le 1+... !
oui oui vous avez raison , n dans |N non |N* , je m'excuse
-
ayalisa
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Nov 2015, 21:18
-
 par ayalisa » 19 Nov 2015, 00:29
par ayalisa » 19 Nov 2015, 00:29
2/image corrigée , je m'excuse
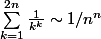
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 19 Nov 2015, 01:58
par Matt_01 » 19 Nov 2015, 01:58
C'est faux. (D'un côté t'as un truc qui converge vers une limite strictement positive, de l'autre côté un truc qui tend vers 0).
EDIT : Je suppose que la somme commence à n.
Du coup le quotient est de type
^{n+k}})
Tu vérifies que n^n/(n+1)^(n+1) tend vers 0, ainsi que n^n/(n+2)^(n+2) et tu utilises que pour k>=3 :
(n+k)^{n+k} = n^(n+k) (1+k/n)^(n+k) >= n^(n+3) et donc n^n/(n+k)^(n+k) <=1/n^2.
Je te laisse justifier la fin.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 19 Nov 2015, 23:22
par aymanemaysae » 19 Nov 2015, 23:22
A l'infini, Sum{k=1 à 2*n} (1/k^k) n'est pas équivalente à 1/n^n :
1) Pour n=50 on a Sum{k=1 à 2*50} (1/k^k) = 1,29128599706266
alors que 1/50^50 = 1,125899906842624 * 10^(-85) .
2) Pour n=100 on a Sum{k=1 à 2*100} (1/k^k) = 1,29128599706266
alors que 1/100^100 = 1 * 10^(-200) .
Donc Sum{k=1 à 2*n} (1/k^k) tend vers 1,29128599706266 quand n tend vers +infini,
et 1/n^n tend vers 0 quand n tend vers +infini.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 118 invités
 (équivalence en +oo)
(équivalence en +oo)
