Un singleton est un fermé.

[HanZel]

Bonjour à tous,
Je voulais savoir si cette démonstration était suffisante.

Soit un espace métrique.
Montrer que tout singleton de est un fermé.

Soit tel que .

On a :

est égal à son adhérence donc est fermé.

Ainsi, tout singleton de est un fermé.

Merci!

[skilveg]

Tu n'as pas justifié que , ce qui est le point-clef du problème! (En fait c'est le problème lui-même!)

Je pense qu'il est plus facile de montrer que le complémentaire d'un point est ouvert.

[HanZel]

D'accord, je vais me pencher sur le complementaire...

Merci.

[skilveg]

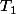
Oui, et même (je crois) qu'un espace est si et seulement si tous ses points sont fermés. Cela dit je ne suis pas sûr que ça aide beaucoup HanZel de savoir ça...

[Bebs]

Est-ce qu'on peut dire que :

Un fermé X est un ensemble dans lequel toute suite convergente à valeurs dans X converge vers une valeur appartenant à cet ensemble X.

Dans ce cas :

Une suite à valeurs dans X = {x} est une suite constante donc elle converge vers x.
Or x appartient à {x} donc toute suite convergente à valeurs dans {x} converge vers une valeur appartenant à {x}.
Donc {x} est fermé.

[skilveg]

Oui, c'est la définition de "séquentiellement fermé" qui est équivalent à "fermé" dans le cas métrique (et plus généralement quand tout point a un système fondamental dénombrable de voisinages, je crois).

En fait tout dépend de la définition que l'on a donnée d'un fermé.

En espérant ne pas dire trop d'âneries...

(Remarque: ce que tu dis est vrai mais pas quand l'espace n'est pas séparé; par exemple pour la topologie grossière toute suite converge vers tout point de l'espace!)

[fourize]

bonjour!

et si on raisonnait par l'absurde !?
on suppose que X est un ouvert. ainsi il existe une boule B(x,µ) ,avec µ positif, appartenant à X . ce qui fera la contradiction !

[zenaf]

Je pense que ce que l'on attend de toi est de prouver que X\{x} est un ouvert. Tu prend un point de cet ensemble, et tu montre qu'il existe autour de ce point une boule de rayon r bien choisie.

[ffpower]

si on parle de boule,c est qu il y a une metrique,et donc dans ce cas la demo de bebs marche aussi(et a mon avis dans cet exo on est en metrique.Si ct de la topo générale,y aurait l hypothese "séparé" dans l énoncé)

[zenaf]

Bonjour à tous,
Je voulais savoir si cette démonstration était suffisante.

Soit un espace métrique.
Montrer que tout singleton de est un fermé.

Je lis simplement l'énoncé... et sinon oui ca marche mais il s'agit la d'une propriété plus que d'une véritable définition c'est pour ca je pense qu'il est important parfois de revenir aux définitions pour bien voir l'objet.

[fourize]

oups!

merci Angelique! de cette rappel !
je pense que la methode du complementaire est la bonne alors !

(je m'y met)

[Nightmare]

Salut à tous !

Et pourquoi pas écrire que ?

[Nightmare]

Pardon, il fallait lire bien sûr et non x.

[kazeriahm]

Que sont ces intervalles dans E ?

[Nightmare]

Oups, je nous croyais sur R. Au temps pour moi.

[HanZel]

je pense que la methode du complementaire est la bonne alors !

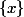
Si est l'union de deux singletons alors le complémentaire de dans est , et est aussi un fermé (ou on tourne en rond...).
Vu comme ça avec le complémentaire, je ne sais pas si ça marche vraiment?

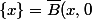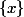
Et est-ce que ne pourrait-on pas simplement écrire ? serait le centre d'une boule fermé de rayon 0=d(x,x).

[HanZel]

Je dirais aussi que puisque c'est le centre d'une boule fermée? C'est valable ca comme raisonnement?

Merci aussi pour toutes vos réponses !

[abcd22]

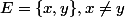
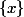
Si est l'union de deux singletons alors le complémentaire de dans est , et est aussi un fermé (ou on tourne en rond...).

Oui, ce n'est pas un problème qu'une partie différente de E et de l'ensemble vide soit à la fois ouverte et fermée, ça veut juste dire que E n'est pas connexe.

Vu comme ça avec le complémentaire, je ne sais pas si ça marche vraiment?

Ben si ça marche.

Et est-ce que ne pourrait-on pas simplement écrire ?

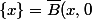Ça ne démontre rien, d'où sort cette égalité ?
Il y a des espaces topologiques (non séparés) où l'adhérence de certains points est l'espace tout entier (chercher « topologie de Zariski » par exemple, ou prendre E = {x, y} avec comme ouverts l'ensemble vide, E et {x} (ce qui est un cas particulier de topologie de Zariski), {x} est un singleton ouvert non fermé et son adhérence est E), donc il y a vraiment quelque chose à montrer pour ton exercice, tu ne peux pas dire comme ça que ça marche parce que ces égalités ont l'air intuitives.