Sin alpha * cos alpha = x : Comment trouver alpha?

par **jemsss** » 13 Avr 2009, 19:57

Bonsoir
Je ne trouve pas comment résoudre une équation de type :

Si on connaît

x comment trouver la valeur de l'angle

?

par **emdro** » 13 Avr 2009, 20:05

Bonsoir,

...?

par **fatal_error** » 13 Avr 2009, 20:32

salut,

tu peux remarquer que

Tu trouves alors

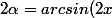apres modulo 2pi ca "devrait" coller (mais je suis pas sur)

par **jemsss** » 13 Avr 2009, 20:42

ok
merci beaucoup

par **Black Jack** » 14 Avr 2009, 13:04

Il manque une famille de solutions.

sin(a).cos(a) = x
sin(2a) = 2x

1°)
2a = arcsin(2x) + 2k.Pi
a = (1/2).arcsin(2x) + k.Pi

2°)
2a = Pi - arcsin(2x) + 2k.Pi
a = Pi/2 - (1/2).arcsin(2x) + k.Pi

Les 2 familles de solutions sont:
a = (1/2).arcsin(2x) + k.Pi
et
a = Pi/2 - (1/2).arcsin(2x) + k.Pi

Avec k dans Z.

Les solutions n'existent que pour x dans [-1/2 ; 1/2]

:zen:

Sin alpha * cos alpha = x : Comment trouver alpha?

sin alpha * cos alpha = x : Comment trouver alpha?

Qui est en ligne