Simplifier multiplication de matrices

[joanie58]

Bonjour!

Soit une matrice X de dimension (nxp) et W une matrice de dimension (nxn) diagonal

Est-ce qu'il y a possibilité de simplifier l'expression suivante?



Ceci est "presque" la matrice de variance-covariance d'un M-estimateur, je me demandais s'il y avait moyen de simplifier l'expression...

Merci!

[Pseuda]

Bonjour,

Tu peux appliquer les 2 propriétés : , que tu peux généraliser avec 3 matrices, et :

[joanie58]

Humm, mais la propriété est vrai si les matrices A et B sont inversibles. Dans mon cas, la matrice X est très rarement de dimension carré et donc très rarement inversible...

[Ben314]

Salut,
A mon avis, on ne peut pas simplifier grand chose.
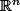
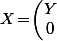En effectuant un changement de base sur (orthonormé pour que ça préserve les transpositions), on peut considérer que où est une matrice pxp inversible.
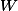
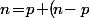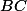
Sauf que, récrite dans cette nouvelle base, il est plus que probable que ne soit plus diagonale, donc en décomposant et avec ces notations, sauf erreur ton bidule donne où la présence du produit laisse peu d'espoir de simplification.

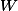
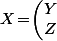Edit : et sans faire de changement de base de façon à garder diagonale, on peut toujours écrire avec pxp et (n-p)xp et je pense que de nouveau, ça ne se simplifie pas outre mesure du fait qu'avec ces notations, la matrice que tu va avoir à inverser se présente sous forme d'une somme de deux matrices.

[fatal_error]

hello,

j'ai une question bête mais...
X'WX est-elle inversible? parce que moyennant qu'on pose L^2 = W, on a L = L' (comme W mais avec des racines carrées)
X'L L X = X'L' L X = U' U avec U = LX, de dim n x p
sauf que U' U c'est pas inversible non?

[Ben314]

Si U est une matrice nxp et qu'elle est de rang p (ce qui implique p<=n) alors U'U sera inversible.
C'est lié au fait que, pour tout vecteur X non nul R^p on a X'U'UX=||UX||² qui est non nul vu que UX est non nul (car U est de rang p) donc U'UX est non nul ce qui signifie que Ker(U'U)={0} et comme U'U est carrée, cela suffit à assurer qu'elle est inversible.
On peut même dire un mieux : U'U est une matrice symétrique définie positive donc diagonalisable dans une base orthonormée et à valeur propres strictement positives.