Le problème, c'est qu'en math, c'est pas du tout super standardisé les notations, mais perso. (en tout cas dans le cours de calcul diff. que je fait), le "d droit", je m'en sert pour désigner la différentielle de l'application, c'est à dire, en reprenant l'exemple çi dessus, que dy (avec un d droit), c'est l'application de R^3 dans L(R^3,R) qui à un (t,x,a) de R^3 associe dy(t,x,a) qui est une application linéaire de R^3 dans R elle même définie par
dy(t,x,a) : R^3->R ; (s,h,b) -> dy(t,x,a)(s,h,b) = 2tx s + (2ax²+t²) h + x² b.
Bref, si

ne dépend que de

alors
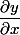
c'est la fonction
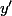
alors que
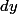
, c'est la fonction qui au réel

associe l'application linéaire (de R dans R)
(h)=f'(x)h)
.
Mais bon, à la place du
(h))
il y a certains auteurs qui mettent un grand D, certain mettent le

et/ou le

en indice, certain écrivent à la fin
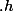
à la place de
)
pour aléger et surtout préciser le coté linéaire de cette dernière "application à

" qui correspond, calculatoirement parlent à un produit matrice par vecteur.
Par exemple, perso, je pense que si on me laisse totalement libre de la notation, j'aurais tendance à écrire
.h)
: différentielle de y (en indice) appliquée à x puis appliqué linéairement à h.
Mais bon, faut évidement savoir s'adapter...
