Serie de Taylor de arctan
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 16 Jan 2007, 19:28
par humpf » 16 Jan 2007, 19:28
Bonsoir, je dois calculer le rayon de convergence de la série:
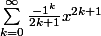
Il est indiqué qu'il faut passer par la série
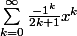
.
J'ai fait ce pas et j'ai trouvé R = -1.
Le problème est que je ne sais pas comment utiliser ce résultat pour arriver à trouver le rayon de convergence de la suite qui est tout en haut :hum: .
Est-ce que quelqu'un peut m'aider?
Merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 16 Jan 2007, 19:37
par Joker62 » 16 Jan 2007, 19:37
Un rayon négatif c'est impossible par définition
Ici le rayon de convergence vaut 1
Pour le trouver, tu dérives termes à termes dans le cercle de convergence et tu vas retomber sur 1 / (1 - (-x²)) qui a un rayon de convergence égale à 1.
De plus une proposition de ton cours dit que la série et la série dérivée ont le même rayon.
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 16 Jan 2007, 20:45
par humpf » 16 Jan 2007, 20:45
Ah oui. Pour le rayon de convergence c'est ok.
Mais alors pour le reste, rien à faire, je comprends pas :hum: .
Tu entends quoi par "cercle de convergence". Je trouve pas dans mon cours ... :triste:
Il faut aussi dire que ce cours est super-résumé et que souvent on n'y trouve pas ce dont on a besoin :hum:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Jan 2007, 20:46
par fahr451 » 16 Jan 2007, 20:46
règle de d 'alembert tu connais ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 16 Jan 2007, 20:50
par Joker62 » 16 Jan 2007, 20:50
Le truc avec la règle de d'Alembert, c'est qu'il faut prendre le rapport des coefficient de deux termes qui se suivent
ici le x ayant comme puissance 2k+1 , on peut pas appliquer la règle de d'Alembert...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Jan 2007, 20:52
par fahr451 » 16 Jan 2007, 20:52
mais si : on n 'applique la règle de d alembert qu 'aux séries numériques et non aux séries entières ( car là avec des séries lacunaires on peut se tromper)
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 16 Jan 2007, 20:54
par humpf » 16 Jan 2007, 20:54
Oui. Alors le cercle de convergence est l'intervalle [0, R]? Dans mon cas [0,1]?
Et après, dériver terme à terme sur ce cercle, c'est à dire dériver seulement les termes 0 et 1?
Je ne comprends pas grand chose ce soir :doh: Si quelqu'un peut m'indiquer un lien où c'est bien expliqué, je veux bien.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 16 Jan 2007, 21:09
par Joker62 » 16 Jan 2007, 21:09
Le rayon de convergence est R = 1
celà veut dire que pour tout x ]-1;1[, il y a convergence absolue
et pour tout x tq |x| > 1, la série diverge.
En ce qui concerne le cas où |x| = 1, (ie le point se trouve sur le cercle) celà dépend. Et le lemme d'Abel est là pour nous aider dans certain cas
Au passage, apparemment t'es à la masse sur les séries entières...
La dérivation termes à termes (resp. l'intégration termes à termes) n'est possible que dans le cercle de convergence.
Par contre je ne vois toujours pas pour la règle de d'Alembert
Elle nous dit juste que si la limite des coefficient de deux termes consécutifs existe alors le rayon de convergence est égale à l'inverse de celle ci,
Ici les deux termes ne sont pas consécutifs... enfin je fais un blocage
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 16 Jan 2007, 22:11
par humpf » 16 Jan 2007, 22:11
Moi aussi je fais un blocage et de taille :hum: !
Alors si j'ai bien compris, je dérive terme à terme dans le rayon de convergence, ce qui me donne
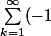^kx^{2k})
Je n'ai toujours pas la série voulue, à savoir
^k}{2k+1}x^{k})
:help:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Jan 2007, 22:16
par fahr451 » 16 Jan 2007, 22:16
pour joker
on utilise la règle de d alembert pour les SERIES NUMERIQUES et non séries entières
u(n) = (-1)^n x^(2n+1) / (2n+1)
pour x non nul
on a l u(n+1)/u(n) l -> lx^2l
la règle de d alembert (merci à elle ) dit
si l x^2l >1 donc silxl>1 il y a divergence
si lxl<1 convergence
donc R = 1
ça marche même quand y a des "trous"
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 17 Jan 2007, 13:34
par Joker62 » 17 Jan 2007, 13:34
Ah ok, ce d'Alembert il en a fait des choses dis donc :D
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Jan 2007, 13:37
par fahr451 » 17 Jan 2007, 13:37
ben oui donc une seule règle de d alembert plutôt que deux dont une qui coince pour les séries lacunaires
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 17 Jan 2007, 13:50
par Joker62 » 17 Jan 2007, 13:50
C'est quoi que tu apelles Séries Lacunaires ???
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 17 Jan 2007, 13:52
par fahr451 » 17 Jan 2007, 13:52
séries entières avec termes manquants, un sur deux un sur trois etc
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 17 Jan 2007, 13:59
par Joker62 » 17 Jan 2007, 13:59
Ah ok j'ai jamais vu ce terme. Bé j'te remercie alors (k)
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 18 Jan 2007, 20:06
par humpf » 18 Jan 2007, 20:06
Je voudrais relancer la discussion à propos du calcul du rayon de convergence de
^k}{2k+1}x^{2k+1})
Ma question est la suivante: sachant que le rayon de convergence de la série no2, à savoir:
^k}{2k+1}x^{k})
est 1, comment "montrer" que le rayon de convergence de la série no1 est aussi 1, sans passer par d'Alembert.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 18 Jan 2007, 20:16
par fahr451 » 18 Jan 2007, 20:16
on factorise par x (ça ne change pas la nature) et on pose u = x^2
on sait que ( cf série 2) qu'il y a cv pour lul <1 et divergence pour lul>1 donc cv pour lxl<1 et div pour lxl>1 donc rayon égal à 1 .
-
humpf
- Membre Relatif
- Messages: 124
- Enregistré le: 01 Nov 2006, 12:53
-
 par humpf » 18 Jan 2007, 20:41
par humpf » 18 Jan 2007, 20:41
D'accord, je crois que j'ai compris (pas à 100% mais pour moi un 80% c'est déjà pas mal...).
Merci :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
