Serie de riemann demo par equivalence

par **adamNIDO** » 20 Déc 2014, 11:47

Bonjour,

ce que je ne comprend pas est ce que si on a une serie a terme positive

donc pour montrer que serie de riemann revient a montrer que suite de terme generale u_n qui est positive est une suite convergente

or on sait que u_n une suite convergente ssi serie télescopique

est convergente

merci pour votre aide

par **zygomatique** » 20 Déc 2014, 12:04

salut

si

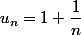
alors u_n converge ....

mais ça m'étonnerait que

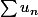
converge ....

par **adamNIDO** » 20 Déc 2014, 12:06

zygomatique a écrit:salut

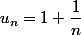
si alors u_n converge ....

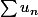
mais ça m'étonnerait que converge ....

alors c'est quoi le principe qui'il sont suivie pour montrer serie de riemann converge

par **capitaine nuggets** » 20 Déc 2014, 13:38

Salut !

Une chose qu'on peut dire :

par **Doraki** » 20 Déc 2014, 14:07

ils disent nulle part que la série des (an) converge <=> la suite (an) converge, ce qui est d'ailleurs complètement faux.

Ils ont utilisé 2 trucs :
si (an) ~ (bn) alors la série des an converge <=> la série des bn converge,
la suite (an) converge <=> la série des (an - a(n-1)) converge

par **adamNIDO** » 20 Déc 2014, 14:20

Doraki a écrit:ils disent nulle part que la série des (an) converge la suite (an) converge, ce qui est d'ailleurs complètement faux.

Ils ont utilisé 2 trucs :
si (an) ~ (bn) alors la série des an converge la série des bn converge,
la suite (an) converge la série des (an - a(n-1)) converge

merci , la suite (an) converge la série des (an - a(n-1)) (telescopique) converge

sil vous plait 2 équivalence nest pas claire pour moi alpha-1 sur n^alpha

par **Doraki** » 20 Déc 2014, 14:39

adamNIDO a écrit:sil vous plait 2 équivalence nest pas claire pour moi alpha-1 sur n^alpha

je comprends rien à ce que tu dis

par **BiancoAngelo** » 20 Déc 2014, 14:45

adamNIDO a écrit:merci , la suite (an) converge la série des (an - a(n-1)) (telescopique) converge

sil vous plait 2 équivalence nest pas claire pour moi alpha-1 sur n^alpha

C'est parce qu'on reprend l'égalité du dessus et qu'on multiplie les équivalents entre eux, sachant bien sûr que :

Et la multiplication donne bien

par **adamNIDO** » 20 Déc 2014, 14:59

BiancoAngelo a écrit:C'est parce qu'on reprend l'égalité du dessus et qu'on multiplie les équivalents entre eux, sachant bien sûr que :

Et la multiplication donne bien

merci beaucoup

par **adamNIDO** » 20 Déc 2014, 16:39

Doraki a écrit:ils disent nulle part que la série des (an) converge la suite (an) converge, ce qui est d'ailleurs complètement faux.

Ils ont utilisé 2 trucs :
si (an) ~ (bn) alors la série des an converge la série des bn converge,
la suite (an) converge la série des (an - a(n-1)) converge

est ce que ces deux trucs valable pour une serie a terme quelconque

par **EGA-SGA** » 20 Déc 2014, 16:47

Pour le premier il faut que a_n soit strict positve (ou négative bien entendu) à partir d'un certain rang, sinon ca peut etre faux.

par **Doraki** » 20 Déc 2014, 16:56

Ah oui merci d'avoir précisé.

Serie de riemann demo par equivalence

serie de riemann demo par equivalence

Qui est en ligne