Série ,partie entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Juin 2007, 18:54
par mehdi-128 » 13 Juin 2007, 18:54
Bonjour,l'exercice consiste a déterminer la nature de la série des 1/a(n) ou:
a(n)=sum(k=1..n)[E(sqrt(k)]
E désignant la partie entière.
En fait,j'ai un peu de mal avec cette partie entière ,je vois pas trop comment faire.
J'ai commencé par écrire:
E(sqrt(k))=p <=> p=
p^2=
Merci....
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 13 Juin 2007, 19:41
par Lierre Aeripz » 13 Juin 2007, 19:41
Il faut d'abord decider, au jugé, si la série est divergente ou convergente. Ici, elle est convergente. Pour le montrer, il faut majorer les

par le terme général d'une série convergente. Cela suffit car les

sont positifs.
Allons-y.
Pour
 \ge x - 1)
.
Pour

, car
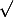
croît.
On a donc, pour

,
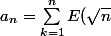 \ge \int_0^n \sqrt{t}dt - n)
Or

Donc
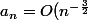)
La série est bien convergente.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités