Série harmonique et divergence

[Charmander]

Bonjour,

Soit la série harmonique.
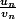
On note l'écriture sous forme de fraction irréductible de celle-ci.
J'aimerais démontrer que les suites et tendent vers

Comme et ne sont pas croissantes, les seules méthodes auxquelles j'ai pensé sont le raisonnement par l'absurde ou le théorème des gendarmes. Par l'absurde ça me paraît bien compliqué, tandis que pour le théorème des gendarmes, j'ai pensé à minorer la suite par n, mais je ne sais pas comment le prouver dans le cas où n n'est pas premier.
Pour la suite u, on remarque qu'elle majore la suite v donc on peut faire les gendarmes une fois qu'on a démontré la divergence pour v.

Voilà, si quelqu'un pourrait m'aider ce serait sympa (si vous avez une autre méthode que l'absurde ou les gendarmes ça me va aussi hein !)
Merci d'avance.

[arnaud32]

deja si un est bornee tu as a et b positifs tels que
donc
qu'en deduis tu pour vn?

[Ben314]

Je suppose que
Concernant Un, il n'y a aucune difficulté vu que Un = Hn x Vn >= Hn qui tend vers l'infini.
Par contre, concernant Vn, je ne vois pas de preuve rapide et élémentaires.
La seule chose qui me vient à l'esprit consiste à utiliser théorème de Tchebychev :
Entre n/2 et n il existe au moins un nombre premier p.
Dans la somme des 1/k pour k de 1 à n, la fraction 1/p sera la seule dont le dénominateur est divisible par p ce qui assure que Vn est divisible par p et donc au moins égal à n/2.

[Charmander]

deja si un est bornee tu as a et b positifs tels que
donc
qu'en deduis tu pour vn?

@arnaud32 Je vois pas ce qu'on peut en déduire de cette inégalité, et puis l'hypothèse un est bornée est fausse non, un et vn ne sont pas bornée puisqu'elles sont censées tendre vers +infini

[Charmander]

Je suppose que
Concernant Un, il n'y a aucune difficulté vu que Un = Hn x Vn >= Hn qui tend vers l'infini.
Par contre, concernant Vn, je ne vois pas de preuve rapide et élémentaires.
La seule chose qui me vient à l'esprit consiste à utiliser théorème de Tchebychev :
Entre n/2 et n il existe au moins un nombre premier p.
Dans la somme des 1/k pour k de 1 à n, la fraction 1/p sera la seule dont le dénominateur est divisible par p ce qui assure que Vn est divisible par p et donc au moins égal à n/2.

Ca me paraît pas mal... Y a moyen de trouver une démonstration simple de ce théorème de Tcherbychev ? Parce que j'ai beau chercher le théorème sur internet, je ne tombe que sur des lois de statistique...

[Ben314]

Effectivement, vu les trés nombreux traveaux de Tchebychef, tu ne tombe pas façilement sur le bon théorème...
J'aurais mieux fait de parler du "postulat de Bertrand"...
http://fr.wikipedia.org/wiki/Postulat_de_Bertrand
La preuve ne demande pas d'outils particulièrement sophistiqués, mais elle n'est pas pour autant "triviale" (en fait c'est un des premiers résultat "non trivial" concernant la répartition des nombres premiers).