"ch(x) et serie de fourier "
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 12 Juin 2009, 14:55
par fourize » 12 Juin 2009, 14:55
bonjour;
le but de developper en serie de fourier la fonction:
l'exercice a écrit:developper en serie de fourier la fonction de 2

_periodique
definie dans l'intervalle[-

,

] par f(x)=ch(x)
il est claire que la fonction est pair donc

=0 ( nul) .
j'ai trouvé

maintenant le probleme est sur :
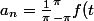 cos(nt) dt)
??
par une integration par partie, ça n'en finit pas ?! :doh:
quelqu'un aurait une idée ? (merci de votre lecture)
* In God we trust, for all others bring data *
-
Black Jack
 par Black Jack » 12 Juin 2009, 15:19
par Black Jack » 12 Juin 2009, 15:19
Et en se rappelant que ch(t) = [e^t + e^(-t)]/2 ?
:zen:
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 12 Juin 2009, 15:20
par Monsieur23 » 12 Juin 2009, 15:20
Aloha ;
Sous forme exponentielle, ça doit bien marcher non ?
« Je ne suis pas un numéro, je suis un homme libre ! »

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 12 Juin 2009, 15:33
par fourize » 12 Juin 2009, 15:33
re,
Monsieur23 a écrit:Aloha ;
Sous forme exponentielle, ça doit bien marcher non ?
j'y crois pas non !
comme ch ; e^(x) n'en finit pas non plus ... :triste: :marteau:
* In God we trust, for all others bring data *
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 12 Juin 2009, 15:38
par Monsieur23 » 12 Juin 2009, 15:38
Mets tout sous forme exponentielle, même le cosinus, non ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Juin 2009, 15:38
par girdav » 12 Juin 2009, 15:38
Bonjour.
On peut calculer
 }dx)
et là la décomposition en exponentielle doit servir.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 12 Juin 2009, 17:51
par Ericovitchi » 12 Juin 2009, 17:51
A mon avis, il faut faire comme dit Black jack.
1) tu transformes le Ch en e^t et e^-t
2) tu intègres par partie en prenant le e^t comme d(e^t)
tu tombes sur un sin(nt) e^t
3) tu intègres une seconde fois par partie et tu retombes sur ton intégrale du début
4) tu la passes de l'autre coté et tu en déduis sa valeur

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 12 Juin 2009, 20:15
par fourize » 12 Juin 2009, 20:15
re,
tout d'abord; merci pour ceux qui ont participé
Ericovitchi a écrit:A mon avis, il faut faire comme dit Black jack.
1) tu transformes le Ch en e^t et e^-t
2) tu intègres par partie en prenant le e^t comme d(e^t)
tu tombes sur un sin(nt) e^t
3) tu intègres une seconde fois par partie et tu retombes sur ton intégrale du début
4) tu la passes de l'autre coté et tu en déduis sa valeur
l'idée m'est venu de cette algorithme :++:
en fait, pas la peine de transformer quoi que ce soit : il suffit juste de remarche que primitive de sh(x) = ch(x) ... par contre je doute sur mon resultat qui est :
^2 \pi -1}{(na)^2 \pi }) = \frac{2}{a \pi} sh(a \pi ) cos(n \pi ))
c'est le ² qui me plait pas: (doute: ne serait il pas la parce que j'ai integrer deux fois? a t il une autre influence ... (si quelqu'un peut me rassurer )
PS. la vraie fonction etait ch(ax) avec a réel. d'ou le a qui traine :zen:
* In God we trust, for all others bring data *
-
Black Jack
 par Black Jack » 13 Juin 2009, 09:01
par Black Jack » 13 Juin 2009, 09:01
Moi, je trouve en final:
}\ .\ sh(a.\pi).cos(n.\pi))
:zen:

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 13 Juin 2009, 12:33
par fourize » 13 Juin 2009, 12:33
re,
Black Jack a écrit:Moi, je trouve en final:
}\ .\ sh(a.\pi).cos(n.\pi))
:zen:
mmhh ! t'as fait une erreur de calcul mon ami :id:
je plaisantes, c'est moi qui me suis trompé. déjà c'est +1 au lieu de -1 dans ma formule. j'ai du perdre d'autre - et + dans mes calcules :briques:
en tout cas; un grand merci à vous tous de votre aide ! :++:
* In God we trust, for all others bring data *
-
kolmogorov
- Membre Naturel
- Messages: 10
- Enregistré le: 14 Juin 2009, 11:06
-
 par kolmogorov » 14 Juin 2009, 11:48
par kolmogorov » 14 Juin 2009, 11:48
bonjour je doit vous donner une astuce our eviter les longues calculs des coéfficient des series de Fourier
rappeler toujous que ch(x) [ecriture à l'aide des exponontielles]
le calcul de l'integrale ;)e^x cos(x)dx ou bien pour le sinus ce fait par partie deux fois...et la méthode reste plus simple.
si vous rencontré ;);)e^ix cos(x)dx , i.e avec la variable comlpexe en utilise toujours le théoreme de Jaurdon relative au calcul des résidus.
Merci.et bonne chance.
 par busard_des_roseaux » 14 Juin 2009, 12:14
par busard_des_roseaux » 14 Juin 2009, 12:14
fourize a écrit: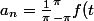 cos(nt) dt)
??
par une integration par partie, ça n'en finit pas ?! :doh:
quelqu'un aurait une idée ? (merci de votre lecture)
cos(nt)=cos(it)cos(nt)=0,5 \left(cos(it-nt)+cos(it+nt) \right))
on primitive:
t)}{i-n} +\frac{sin((i+n)t)}{i+n} \right)) remarque
remarque: sin(z) est définie par sa série

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 14 Juin 2009, 15:09
par fourize » 14 Juin 2009, 15:09
re,
kolmogorov a écrit:si vous rencontré

;)e^ix cos(x)dx , i.e avec la variable comlpexe en utilise toujours le théoreme de Jaurdon relative au calcul des résidus.
Merci.et bonne chance.
- je n'ai pas vu ce calcule de residu même je le lis souvent dans ce forum (avance...) tu pourrais m'expliquer ce que c'est ? (merci)
* pour busard_de_reseaux:
tu veux dire que
 = cos(it))
???????? :doh:
* In God we trust, for all others bring data *
 par Dominique Lefebvre » 14 Juin 2009, 15:13
par Dominique Lefebvre » 14 Juin 2009, 15:13
kolmogorov a écrit:si vous rencontré

;)e^ix cos(x)dx , i.e avec la variable comlpexe en utilise toujours le théoreme de Jaurdon relative au calcul des résidus.
Merci.et bonne chance.
Bonjour,
Le théorème de Jaurdon : c'est nouveau ça vient de sortir? Ce n'est pas plutôt le lemme de Jordan?
 par busard_des_roseaux » 14 Juin 2009, 15:42
par busard_des_roseaux » 14 Juin 2009, 15:42
fourize a écrit:ch(x) = cos(ix) ???????? :doh:
bah, vi
=\frac{e^{i(it)}+e^{ -i(it)}}{2}=ch(t))
les 5 (sin,cos,ch,sh,exp) ont à peu près la même définition via les séries
de la variable z
=cos(z) \\<br />cos(iz)=ch(z) \\<br />sin(iz)=ish(z) \\<br />sh(iz)=isin(z) \\<br />cos(z)=0,5 \left( exp(iz)+exp( -iz) \right) \\<br />ch(z)=0,5 \left( exp(z)+exp( -z) \right))
ce qui change vraiment, c'est l'absence de

en trigonométrie hyperbolique (??????). :we:

semble être une "constante de platitude".

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 14 Juin 2009, 19:20
par fourize » 14 Juin 2009, 19:20
merci pour tout ces détails busard_des_reseaux
c'etait nulle comme question :marteau: mais je n'avais pas un couteau sous la main
:zen: thanks :zen:
* In God we trust, for all others bring data *
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
_periodique
,
] par f(x)=ch(x)
