À la physicienne, on veut caractériser la propension qu'ont les lignes du champ F à tourner autour du point M(x,y,z) au moyen d'un objet qui ne dépend que des dérivées premières de F en M : (rot F)(M). On veut que la première coordonnée de (rot F)(M) donne la propension qu'ont les lignes de champ de F à tourner autour de l'axe Mx en M, que la deuxième coordonnée décrive la rotation des lignes de champ autour de l'axe My et la troisième, autour de l'axe Mz.
Prenons par exemple la troisième coordonnée, l'idée c'est que la propension des lignes à tourner autour de M et de l'axe Mz est donnée par la circulation de F sur un petit contour qui tourne autour de M dans le plan Mxy. On prend donc une petite longueur dl et le petit carré C : (x,y,z) -> (x+dl,y,z) -> (x+dl,y+dl,z) -> (x,y+dl,z) -> (x,y,z) et on définit la troisième coordonnée de (rot F)(M) par
(M).\vec{e_z} = \frac{1}{dl^2}\oint_C \vec{F}.\vec{dl})
(le facteur dl² c'est pour avoir un truc homogène).
En supposant que dl est suffisamment petit pour que les dérivées premières de F soient constantes à l'intérieur de C, c'est-à-dire que pour tout (x',y') dans [x,x+dl]x[y,y+dl] on a F(x',y',z) = F(M) + dF/dx(M)(x'-x) + dF/dy(M)(y'-y), on peut calculer l'intégrale circulante et on tombe sur le bien connu
(M).\vec{e_z} = \frac{\partial F_y}{\partial x}(M) - \frac{\partial F_x}{\partial y}(M))
avec Fx et Fy les première et deuxième coordonnées de F.
D'où la définition du rotationnel en coordonnées cartésiennes que tu connais, et qui vérifie pour tout contour fermé C encerclant une surface S
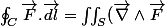.\vec{dS})
, qui est une généralisation de l'égalité plus haut.
