Bonsoir,
Je rencontre une difficulté sur un exercice assez élémentaire. Cela m'agace quelque peu.
Voici l'exercice:
Résoudre les équations suivantes, d’inconnue P ∈ R[X] :
X^2P"+ 2XP' − 2P = 0
X^2P" + 2XP' - P = 0
J'ai posé P = anX^n + ... + a0 avec (an,...,a0) appartenant à R
J'ai dérivé P deux fois pour avoir P' et P" puis j'ai remplacé dans les expressions de départ. Après cela, je ne vois pas comment faire pour déterminer P. Je pensais aller du côté du degré de P.
En faisant ça, j'ai développé les expressions de départ en remplaçant P, P' et P".
J'ai essayé d'isoler X^n afin d'avoir le degré de P mais ça ne mène pas bien loin...
Je suis en panne d'inspiration...
Merci d'avance pour votre aide !
Résoudre une équation d'inconnue P appartenant à R[X]
11 messages
- Page 1 sur 1
Re: Résoudre une équation d'inconnue P appartenant à R[X]
thoralf8weblen a écrit:J'ai essayé d'isoler X^n afin d'avoir le degré de P mais ça ne mène pas bien loin...
Qu'obtiens-tu ?
Mon 6000ème message


Re: Résoudre une équation d'inconnue P appartenant à R[X]
J'obtiens:
[an*n*(n-1) +2(an)*n - 2(an)]X^n pour la première équation
[an*n*(n-1) +2(an)*n - an]X^n pour la deuxième équation.
les an correspondent aux coefficients devant les X^n.
[an*n*(n-1) +2(an)*n - 2(an)]X^n pour la première équation
[an*n*(n-1) +2(an)*n - an]X^n pour la deuxième équation.
les an correspondent aux coefficients devant les X^n.
Re: Résoudre une équation d'inconnue P appartenant à R[X]
C'est bien ce que j'ai fait...
Je tombe, pour la deuxième sur an[n^2 + n - 1]. Je pense que je bute sur une évidence car je ne vois pas la simplification...
Je tombe, pour la deuxième sur an[n^2 + n - 1]. Je pense que je bute sur une évidence car je ne vois pas la simplification...
Re: Résoudre une équation d'inconnue P appartenant à R[X]
thoralf8weblen a écrit:Je tombe, pour la deuxième sur an[n^2 + n - 1]
Egal quoi ?
Re: Résoudre une équation d'inconnue P appartenant à R[X]
Egal 0...
an différent de 0 sinon on aurait le polynôme nul. Donc n^2 +n - 1 = 0 . Je bloque sur n^2 +n = 1.
an différent de 0 sinon on aurait le polynôme nul. Donc n^2 +n - 1 = 0 . Je bloque sur n^2 +n = 1.
Re: Résoudre une équation d'inconnue P appartenant à R[X]
n est un entier
Est-ce que n²+n-1 peut être nul ?
Est-ce que n²+n-1 peut être nul ?
Re: Résoudre une équation d'inconnue P appartenant à R[X]
Si n^2 + n = 1, la réponse est non. Mais si n^2 + n -1 est non nul, alors an est nul car nous sommes sur un aneau intègre. Or an n'est pas nul par définition...
Re: Résoudre une équation d'inconnue P appartenant à R[X]
Je conseille de traiter les cas des "petites" (0 et 1) puissances de X à part car les dérivées secondes sont nulles.
Si je prends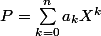
Pour k=0, on obtient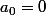
Pour k=1, on obtient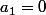
Et pour k=2 à n, on obtienta_k = 0) donc
donc 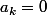 puisque
puisque 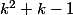 ne peut pas être nul.
ne peut pas être nul.
Ce qui signifie que la seule solution est le polynôme nul.
Reste à traiter la 1ère équation.
Si je prends
Pour k=0, on obtient
Pour k=1, on obtient
Et pour k=2 à n, on obtient
Ce qui signifie que la seule solution est le polynôme nul.
Reste à traiter la 1ère équation.
Re: Résoudre une équation d'inconnue P appartenant à R[X]
Oui, je crois que je me suis emmêlé les pinceaux avec les deux équations à force d'essayer de les résoudre. Je comprends. Merci beaucoup !
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
