Bonjour,
j'aimerais savoir comment résoudre cette équation :
|x| +√(−x) =6
or je ne sais pas comment m'y prend, j'ai bien trouvé un resultat ou x=4 en faisant de tête et en cherchant sur internet mais je n'ai toujours pas comment comment le faire. Si vous pouvez m'aider,
Merci
Résoudre équation
6 messages
- Page 1 sur 1
Re: Résoudre équation
Comme ont sait qu'une racine carrée ne peut pas être négative donc ça veut dire que le x dans la racine est négatif donc √(- -x) = √(x):
donc |-x| + √(x) =6
Je sais pas si je réponds à ta question.
Après à part avoir trouvé ceci je ne voie pas quoi faire d'autre
donc |-x| + √(x) =6
Je sais pas si je réponds à ta question.
Après à part avoir trouvé ceci je ne voie pas quoi faire d'autre
Re: Résoudre équation
x étant négatif , l'équation devient -x+
je vois deux méthodes :
1 .-4 est solution
on pose f(x)=-x+
f est somme de deux fonctions strictement décroissantes sur R_ donc f est strictement décroissante.
-4est donc la seule solution de l'équation .
2.Si x est solution , alors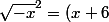^2)
donc et donc x appartient à {-9;-4}
et donc x appartient à {-9;-4}
Il suffit ensuite de tester ces nombres .
je vois deux méthodes :
1 .-4 est solution
on pose f(x)=-x+
f est somme de deux fonctions strictement décroissantes sur R_ donc f est strictement décroissante.
-4est donc la seule solution de l'équation .
2.Si x est solution , alors
donc
Il suffit ensuite de tester ces nombres .
Re: Résoudre équation
D'accord je voie ton raisonnement mais tu t'es trompé sur l'équation, il y a une valeur absolue donc l'équation dans ce cas ne devient pas |-x|+ √(x) =6 -> x+√(x) =6 ? sauf si je me trompe, je crois que c'est bien ça
En tout cas merci pour ta réponse.
En tout cas merci pour ta réponse.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
