Résolvante compacte
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 18 Mar 2018, 11:07
par Sylvain200 » 18 Mar 2018, 11:07
Bonjour,
Pouvez vous m'aider à prouver l'équivalence suivante:
Si A est un opérateur non borné dans un Hilbert

de domaine
)
(
)
est
muni de sa norme du graphe), et tel que l'ensemble résolvant
\neq \emptyset)
, alors on a

est à résolvante compacte si et seulement si
)
s'injecte d'une manière compacte dans

.
Merci d'avance.
-
aviateur
 par aviateur » 18 Mar 2018, 11:44
par aviateur » 18 Mar 2018, 11:44
Bonjour
Soit

dans l'ensemble résolvant, on note pour simplifier
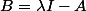
On a donc
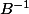
est un opérateur borné de H vers D(A).
Soit
)
une suite ds la boule unité de H, la suite
)
est une suite bornée dans D(A) et
si D(A) s'injecte de façon compacte ds H, on peut extraire une sous suite de
)
qui cv dans H, i.e
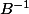
est un opérateur compact.
La réciproque est du même gabarit.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 18 Mar 2018, 12:26
par Sylvain200 » 18 Mar 2018, 12:26
Merci bien pour votre réponse.
Pourquoi
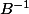
est un opérateur borné de

vers
)
?
Je pense qu'il est borné de

dans

. Me trompe-je?
Pour montrer que
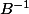
es compact, on doit montrer l'existence d'une sous suite de
)
qui converge dans
)
ou dans

?
-
aviateur
 par aviateur » 18 Mar 2018, 16:03
par aviateur » 18 Mar 2018, 16:03
Rebonjour
Non tu ne te trompes pas. Mais si

est borné pour la topologie de H, il l'est aussi pour la topologie de D(A).
En effet
}=||u||_H+||Tu||_H\leq ||u||_H+c||u||_H =(c+1)||u||_H)
Pour ta seconde question tu veux vérifier que T est compact comme opérateur de H dans H
donc d'une suite x_n bornée dans H tu dois pouvoir extraire une sous-suite Tx_n qui cv dans H
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 18 Mar 2018, 16:58
par Sylvain200 » 18 Mar 2018, 16:58
Merci très bien aviateur.
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 18 Mar 2018, 17:20
par Sylvain200 » 18 Mar 2018, 17:20
aviateur a écrit:Rebonjour
Non tu ne te trompes pas. Mais si

est borné pour la topologie de H, il l'est aussi pour la topologie de D(A).
En effet
}=||u||_H+||Tu||_H\leq ||u||_H+c||u||_H =(c+1)||u||_H)
Excusez moi aviateur, mais c'est pas ça la norme de
})
.
Ce que vous avez écrit, c'est la norme
})
.
-
aviateur
 par aviateur » 18 Mar 2018, 22:57
par aviateur » 18 Mar 2018, 22:57
Rebonjour
Oui effectivement je corrige et dis moi si tu es d'accord.
}=||Tu||_H+||ATu||_H)
mais
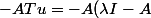^{-1}u=(\lambda I-A)(\lambda I-A)^{-1}u-(\lambda I-A)^{-1}u=(I-T)u)
Donc

Finalement
}=||Tu||_H+||ATu||_H\leq (1+2c)||u||_H)
-
Sylvain200
- Membre Naturel
- Messages: 25
- Enregistré le: 13 Déc 2016, 17:09
-
 par Sylvain200 » 19 Mar 2018, 07:09
par Sylvain200 » 19 Mar 2018, 07:09
Bonjour,
Ok je suis d'accord, juste une petite correction c'est
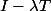
au lieu de
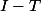
.
Merci beaucoup.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
est borné pour la topologie de H, il l'est aussi pour la topologie de D(A).