C'est là le problème, cette intégrale ne vaut pas zéro.
Je crois qu'il est impossible de remplacer la somme par la fonction zeta, car 0<Re(s)<1. Dans ce cas-là, en plus de n'être exploitable que lorsque Re(s)>1, la forme de sommation des inverses de la zeta de Riemann ne serait valable que pour Re(s)>1. Si la substitution de cette somme par ζ(s) était permise, alors cette équation n'aurait pas de solution selon les procédés que j'ai employés.
Pour calculer cette intégrale, j'ai essayé de dériver
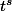
à partir de la forme développée des puissances complexes (que l'on obtient avec quelques changements de formes)
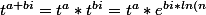}=t^{a}*(cos(b*ln(t))+i*sin(b*ln(t))))
Selon cette formule, il me semble avoir correctement calculé par dérivation de fonctions composées (mais il faut absolument que j'aille revérifier plus rigoureusement), que la dérivée de
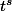
est égale, par une heureuse coincidence et similairement à des puissances réelles, à
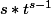
En reprenant notre intégrale de
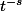
, on la multiplie par
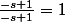
et on fait passer le numérateur dans l'intégrale. On cherche alors
t^{-s}dt})
.
Si on applique la formule de la dérivée de
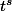
, alors une primitive de
t^{-s})
serait
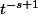
. On admet que, dans les complexes, on peut aussi calculer une intégrale à l'aide de deux valeurs de la primitive, et on a
t^{-s}dt}=\frac{1}{-s+1}*\lim_{x\rightarrow\infty}\int_{0}^{x}{(-s+1)t^{-s}dt}=\frac{1}{-s+1}*\lim_{x\rightarrow\infty}(x^{-s+1}-\lim_{t\rightarrow0}t^{-s+1}))
On trouve
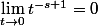
Soit
=\frac{1}{-s+1}*\lim_{x\rightarrow\infty}x^{-s+1}=\lim_{x\rightarrow\infty}\frac{x^{-s+1}}{-s+1})
Donc, à la fin, on a
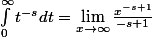
C'est ainsi que je calcule cette intégrale.
Mon équation devient donc
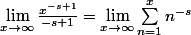
Pour vérifier expérimentalement cette équation pour une certaine valeur de s, j'entre alors la différence de ces deux membres en tant que fonction dans ma calculatrice et je vérifie, pour des valeurs de x croissantes, que la différence des deux se rapproche de 0 (ou semble s'en rapprocher, au vu des imprécisions).
