Bonjour, on a vu en td qu'une matrice A associer un un endomorphisme f, est semblable à sa matrice diagonaliser ( la matrice avec les val. propres sur la diag et rien d'autre) et que la matrice de passage était la réunion des vecteurs des bases des sous espaces propres . Mais pourquoi la matrice de passage est composé des vecteurs des sous espace propres ??? j'arrive pas à avoir l'intuition.
PS: je suis en prépa TSI, je viens d'un bac technologique c'est pour ça que je galère avec un truc qui peut vous sembler trivial mdrr
Réduction d'endomorphisme
4 messages
- Page 1 sur 1
Re: Réduction d'endomorphisme
Bonjour,
As-tu vu la notion de changement de base pour la matrice d'un endomorphisme, comment y intervient la matrice de changement de base et comment est fabriquée la matrice de changement de base ?
C'est exactement ce qui intervient ici pour la diagonalisation : on change de base pour écrire la matrice de l'endomorphisme dans une base de vecteurs propres pour
dans une base de vecteurs propres pour  (quand une telle base existe, c.-à-d. quand l'endomorphisme
(quand une telle base existe, c.-à-d. quand l'endomorphisme  est diagonalisable).
est diagonalisable).
As-tu vu la notion de changement de base pour la matrice d'un endomorphisme, comment y intervient la matrice de changement de base et comment est fabriquée la matrice de changement de base ?
C'est exactement ce qui intervient ici pour la diagonalisation : on change de base pour écrire la matrice de l'endomorphisme
Re: Réduction d'endomorphisme
oui on a vu ça. Ce que je ne comprends pas, c'est pourquoi PAP-1
= D , marche quand P est composé des vecteurs des bases des sous espace propres . Comment ils apparaissent. Parcequ'en cours la prof a juste dis qque c'était la methode et quand je lui est demandé, elle m'a dit de revoir mon cours...
= D , marche quand P est composé des vecteurs des bases des sous espace propres . Comment ils apparaissent. Parcequ'en cours la prof a juste dis qque c'était la methode et quand je lui est demandé, elle m'a dit de revoir mon cours...
Re: Réduction d'endomorphisme
C'était sûrement un bon conseil de revoir ton cours. Déjà, la formule de changement de base est à revoir.
 est la matrice d'un endomorphisme
est la matrice d'un endomorphisme  dans la base
dans la base 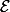 .
.
 est la matrice de passage de la base
est la matrice de passage de la base 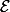 à la base
à la base 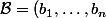) de vecteurs propres qu'on a trouvée. Donc
de vecteurs propres qu'on a trouvée. Donc 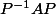 (et pas
(et pas 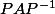 !) est la matrice de l'endomorphisme dans la base
!) est la matrice de l'endomorphisme dans la base 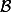 .
.
Maintenant réfléchis à ce qu'est cette matrice. Soit la valeur propre associée au vecteur propre
la valeur propre associée au vecteur propre  . Alors
. Alors = {?}) . Et donc la matrice
. Et donc la matrice 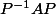 est ...
est ...
Maintenant réfléchis à ce qu'est cette matrice. Soit
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 132 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
