Reduction endomorphisme

[Madi47]

Bonjour a tous,


Comment fait on pour montrer qu un plan est stable par un endomorphisme associe a sa matrice

par exemple un plan d equation y+z=0 est il stable par f endo de R3 canoniquement associe a la matrice

M= 110
-121
101

comment le montrer ? de meme pour la droite vect((1,1,1))?

merci a tous.

[capitaine nuggets]

Salut !

Bonjour a tous,


Comment fait on pour montrer qu un plan est stable par un endomorphisme associe a sa matrice

par exemple un plan d equation y+z=0 est il stable par f endo de R3 canoniquement associe a la matrice

M= 110
-121
101

comment le montrer ? de meme pour la droite vect((1,1,1))?

merci a tous.

Si j'appelle ton plan alors est stable par si :+++:

[zygomatique]

salut

certes oui ....

il suffit de prendre une base du plan, de calculer son image et de vérifier qu'elle appartient au plan ...

[Ben314]

Salut,
A la limite, si tu as un peu plus de "bagage" en algèbre linéaire, ton plan P a pour équation avec ici (et ).
Si tu prend d'un vecteur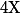 de R^3, son image par ton endomorphisme est et cette image est dans P ssi .
Pour que cette condition soit équivalente à (i.e. équivalente au fait que X est lui même dans le plan P), il faut et il suffit que et soit colinéaires, c'est à dire (en passant aux transposés) que et soit colinéaires ce qui est très facile à vérifier.
Et ça signifie en fait, que doit être un vecteur propre de la matrice et on peut retrouver ainsi les liens (un peu compliqués) qu'il y a entre les vecteurs propres de 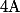et ceux de .

[Madi47]

Salut,
A la limite, si tu as un peu plus de "bagage" en algèbre linéaire, ton plan P a pour équation avec ici (et ).
Si tu prend d'un vecteur de R^3, son image par ton endomorphisme est et cette image est dans P ssi .
Pour que cette condition soit équivalente à (i.e. équivalente au fait que X est lui même dans le plan P), il faut et il suffit que et soit colinéaires, c'est à dire (en passant aux transposés) que et soit colinéaires ce qui est très facile à vérifier.
Et ça signifie en fait, que doit être un vecteur propre de la matrice et on peut retrouver ainsi les liens (un peu compliqués) qu'il y a entre les vecteurs propres de et ceux de .

Bonjour,


Si je redige ainsi est ce correct?

Soit u=(x,y,z) de R3 u appartient a P ssi y=-z
ssi u=(x,y,-y)
ssi u=x(1,0,0)+y(0,1,-1)

on obtient une famille de vecteur generatrice et libre. Je pose v1= (1,0,0) et v2= (0,1,-1)

et je calcule MV1= (1,-1,1) d ou f(v1)=v1-v2

MV2=(1,2,-1) d ou f(v2)=v1+v2 tous deux elements de P donc P est stable par f??????

j espere que ce que j ai ecris n est pas du charabia....

[zygomatique]

oui c'est une méthode ...

sauf que es-tu sur que f(v2) = v1 + v2 ?

ensuite tu peux directement calculer Mu (avec u = (x, y, -y)

....