Bonjour,
j'ai un polynôme défini tel que
P0(x)=2, P1(X)=x
pour tout n >= 2, Pn+1(x) = x * Pn(x) - 1/4 Pn-1(x)
Dans une question je devais calculer Pn(1), Pn(-1) et Pn(0)
j'ai conjecturé :
Pn(1)=2^(n-1)
Pn(-1)=(-1)^n * 2^(n-1)
Pn(0)=(-1)^n*2^(n-1) si n pair
Pn(0)=0 si n impair
mais je ne vois pas comment le démontrer...
mais c'est après que je suis complètement perdu : je dois démontrer que Pn(x) = ( 1 / 2^(n-1) ) * cos(n*theta) avec theta=Arccos(x) et x dans [-1;1]
est-ce que vous avez une idée ?
Merci d'avance
Récurrence et trigo
9 messages
- Page 1 sur 1
Je suppose que pour Pn(1), tu as conjecturé Pn(1)=2^(1-n) et pas 2^(n-1), sinon, c'est sûr que c'est difficile à montrer. (j'ai pas vérifié les autres calculs, mais j'ai l'impression qu'il y a d'autres fautes du même genre : vérifie au rang 0...)
Sinon, je crois qu'il n'y a pas forcément besoin de conjecturer : tu as=P_{n+1}(1)-P_{n}(1)/4) donc une récurrence linéaire d'ordre 2 (fais de même avec -1 et pour 0, c'est encore plus simple). Tu peux donc en déduire les résultats.
donc une récurrence linéaire d'ordre 2 (fais de même avec -1 et pour 0, c'est encore plus simple). Tu peux donc en déduire les résultats.
La deuxième question doit se faire par récurrence mais là, désolé, j'ai pas le temps de l'expliquer (p'têt demain si personne ne t'aide ...)
Sinon, je crois qu'il n'y a pas forcément besoin de conjecturer : tu as
La deuxième question doit se faire par récurrence mais là, désolé, j'ai pas le temps de l'expliquer (p'têt demain si personne ne t'aide ...)
Paulo > Bien vu :p T'as réussi toi ?
boulay59 > Oups, désolé, c'est 1-n pour les 3 conjectures en effet :
Pn(1)=2^(1-n)
Pn(-1)=(-1)^n * 2^(1-n)
Pn(0)=(-1)^n*2^(1-n) si n pair
Pn(0)=0 si n impair
Sinon, je crois bien que j'ai jamais vu de récurrences d'ordre 2, et je vois pas comment on peut déduire ce que j'ai conjecturé à partir de cette relation :-\
boulay59 > Oups, désolé, c'est 1-n pour les 3 conjectures en effet :
Pn(1)=2^(1-n)
Pn(-1)=(-1)^n * 2^(1-n)
Pn(0)=(-1)^n*2^(1-n) si n pair
Pn(0)=0 si n impair
Sinon, je crois bien que j'ai jamais vu de récurrences d'ordre 2, et je vois pas comment on peut déduire ce que j'ai conjecturé à partir de cette relation :-\
Vous avez pas encore fait les récurrences linéaires d'ordre 2 (et supérieur bien sûr) !!! Et ben décidément, on fait vraiment plus rien en prépa... :lol3:
Non, sérieusement, comme tu n'as pas vu cette méthode de résolution "rapide" (enfin ça dépend), on va le faire comme tu as commencé, par conjecture puis démonstration par récurrence :
Tu as=P_{n+1}(1)-P_{n}(1)/4)
Soit=2^{1-n})
Alors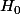 et
et 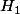 sont vrais
sont vrais
On suppose pour donné que
donné que 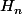 et
et 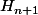 sont vrais et tu démontres
sont vrais et tu démontres  :
:
On a=P_{n+1}(1)-P_{n}(1)/4)
Donc d'après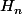 et
et 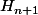 ,
, =2^{1-(n+1)}-2^{1-n}/4=2^{-n}-2^{-n-1}=2^{-n-1}=2^{1-(n+2)})
Donc est vérifié
est vérifié
CQFD
Non, sérieusement, comme tu n'as pas vu cette méthode de résolution "rapide" (enfin ça dépend), on va le faire comme tu as commencé, par conjecture puis démonstration par récurrence :
Tu as
Soit
Alors
On suppose pour
On a
Donc d'après
Donc
CQFD
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
